5 Construindo Topologias

Capítulo 5
Construindo Topologias

5.1 Comparando Topologias

Em um mesmo conjunto $X$ , podemos ter deﬁnidas duas topologias $τ_{1}$ e $τ_{2}$ . Pode acontecer que $τ_{1} \subset τ_{2}$ , por exemplo. Neste caso, sempre que $f : (X, τ_{X}) \to (Y, τ_{Y})$ for contínua, teremos que $f : (X, τ_{2}) \to (Y, τ_{Y})$ também será contínua. Também podemos concluir que

x_{n} \to_{}^{τ_{2}} x \Rightarrow x_{n} \to_{}^{τ_{1}} x .

Pode ser que não tenhamos nem $τ_{1} \subset τ_{2}$ , nem $τ_{2} \subset τ_{1}$ . Duas topologias nem sempre são comparáveis.

Deﬁnição 5.1.

Se $(X, τ_{X})$ e $(X, τ_{X})$ são duas topologias em um mesmo conjunto $X$ e $τ_{1} \subset τ_{2}$ , então dizemos que $τ_{2}$ é mais forte ou mais ﬁna que $τ_{1}$ . Também dizemos que $τ_{1}$ é mais fraca que $τ_{2}$ . Podemos também dizer que $τ_{1}$ é menor que $τ_{2}$ , ou que $τ_{2}$ é maior que $τ_{1}$ . Veja a Observação 5.3.

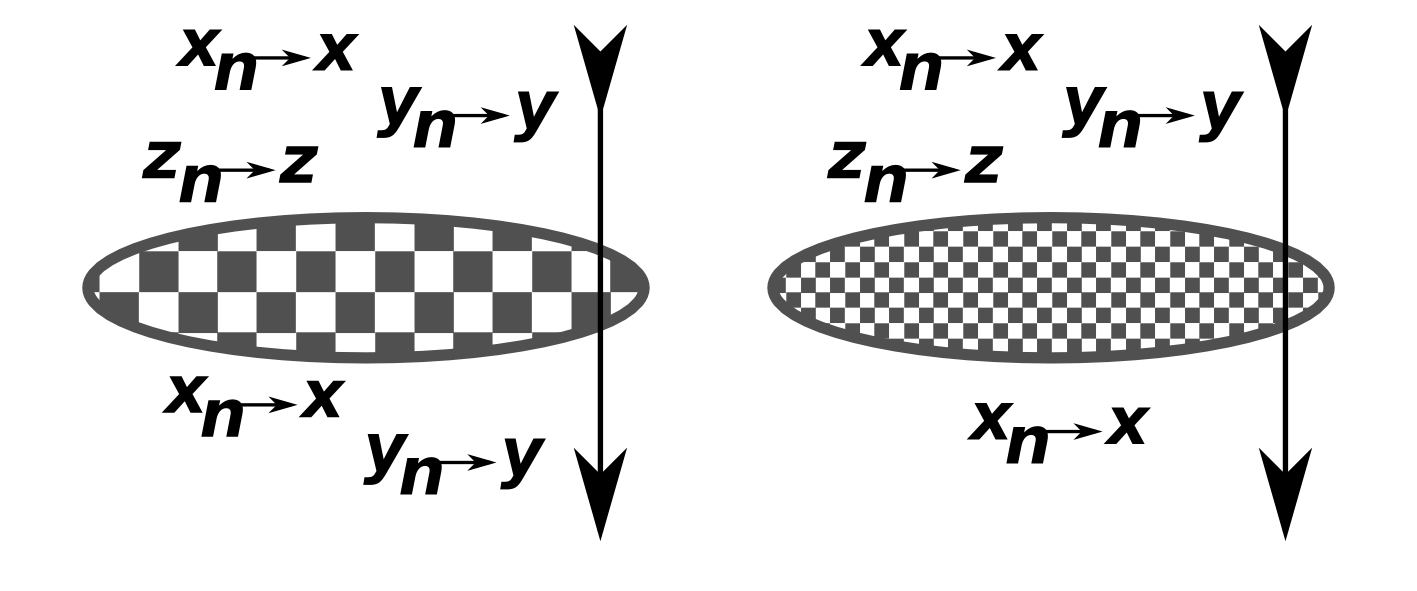
A topologia determina quais são as sequências que convergem e quais não convergem. Se imaginarmos a topologia como uma “peneira” que deixa passar apenas as sequências convergentes, quanto mais ﬁna for a topologia, menos sequências passarão como convergentes. Veja a Figura 5.1.

Figura 5.1: Quanto mais ﬁna é a topologia, menos sequências “passam” como convergentes.

Proposição 5.2.

Seja $X$ um conjunto qualquer, e $τ_{λ}$ $(λ \in Λ)$ uma família de topologias em $X$ . Então $τ_{X} = ⋂_{λ \in Λ} τ_{λ}$ é uma topologia em $X$ .

Demonstração. Basta veriﬁcar que $τ_{X}$ satisfaz os axiomas listados na Deﬁnição 4.1. Por exemplo,

\begin{array}{l} A, B \in τ_{X} & \Rightarrow \forall λ \in Λ, A \cap B \in τ_{λ} \\ \Rightarrow A \cap B \in ⋂_{λ \in Λ} τ_{λ} = τ_{X} . \end{array}

□

Observação 5.3.

A relação “mais forte que” deﬁne uma ordem parcial na família

𝒯 (X) = \{τ_{X} \subset 𝒫 (X)| τ_{X} é topologia\},

das topologias de um conjunto $X$ . Esta ordem é simplesmente a restrição da relação de inclusão deﬁnida em $𝒫 (X)$ à família $𝒯 (X)$ .

Existe um elemento máximo dentre todas as topologias de $X$ . É o conjunto das partes de $X$ , $𝒫 (X)$ , que é a topologia mais forte que pode ser deﬁnida em $X$ . Por outro lado, ${\emptyset, X}$ é a topologia mais fraca em $𝒯 (X)$ .

A Proposição 5.2 mostra que dada uma família de topolgias $τ_{λ} (λ \in Λ)$ , existe a maior topologia que é menor que todas as $τ_{λ}$ . Essa topologia $τ_{δ}$ é o ínﬁmo das $τ_{λ}$ . Escrevemos

τ_{δ} = \land \{τ_{λ}| λ \in Λ\} .

τ_{δ} = \underset{λ \in Λ}{\land} τ_{λ} .

Por outro lado, a união de topologias não é necessariamente uma topologia. No entanto, se considerarmos a família

ℱ = \{τ_{X} \in 𝒯 (X)| ⋃_{λ \in Λ} τ_{λ} \subset τ_{X}\}

de todas as topologias que são maiores que todas as $τ_{λ}$ , sabemos que a família $ℱ$ não é vazia, pois $𝒫 (X) \in ℱ$ . Seja então $τ_{σ}$ o ínﬁmo de $ℱ$ :

τ_{σ} = \land ℱ .

A topologia $τ_{σ}$ é a menor topologia que é maior que todas as $τ_{λ}$ . Essa topologia é o supremo de $τ_{λ}$ , e é denotada por

τ_{σ} = \underset{λ \in Λ}{\lor} τ_{λ} .

5.1.1 Comparação de Topologias e Continuidade

Quando $X$ é um espaço topológico dotado de duas topologias $τ_{1}$ e $τ_{2}$ , o que podemos dizer da relação entre essas topologias se soubermos que a aplicação identidade

\begin{matrix} id : & (X, τ_{1}) & \to & (X, τ_{X}) \\ x & \mapsto & x \end{matrix}

é contínua? A resposta é simples:

id é contínua \Leftrightarrow τ_{2} \subset τ_{1} .

Vamos generalizar isso para uma aplicação qualquer

f : (X, τ_{1}) \to (X, τ_{X}) .

Proposição 5.4.

Seja $X$ um conjunto qualquer e $(Y, τ_{Y})$ um espaço topológico. Dada uma aplicação qualquer $f : X \to Y$ , $τ_{f} = f^{- 1} (τ_{Y})$ deﬁne uma topologia em $X$ .

Demonstração. Basta notar que $\emptyset, X \in τ_{f}$ , se $A, B \in τ_{f}$ , então $A = f^{- 1} (A^{'})$ e $B = f^{- 1} (B^{'})$ com $A^{'}, B^{'} \in τ_{Y}$ . Como $τ_{Y}$ é uma topologia, $A^{'} \cap B^{'} \in τ_{Y}$ . Assim, $A \cap B = f^{- 1} (A^{'} \cap B^{'}) \in f^{- 1} (τ_{Y}) = τ_{f}$ . Podemos fazer analogamente para a união arbitrária de elementos de $τ_{f}$ . Basta observar que $f^{- 1} : 𝒫 (Y) \to 𝒫 (X)$ comuta com as operações de união e interseção. □

Pela Proposição 5.4, dizer que $f : (X, τ_{X}) \to (Y, τ_{Y})$ é contínua é o mesmo que dizer que a topologia $τ_{f}$ é mais fraca que $τ_{X}$ . De fato, é fácil veriﬁcar que $τ_{f}$ é a menor topologia que faz com que $f : X \to (Y, τ_{Y})$ seja contínua.

5.2 Sub-Base

A construção feita na Observação 5.3 é muito comum. É essa construção que em álgebra, por exemplo, nos permite deﬁnir para um espaço vetorial $V$ e um subconjunto qualquer $S \subset V$ , o menor subespaço de $V$ que contém $S$ . Este é o subespaço vetorial gerado por $S$ . Do mesmo modo, para um grupo $G$ e um subconjunto qualquer $S \subset G$ , pode-se deﬁnir o que seria o grupo gerado por $S$ . Esse seria o menor subgrupo de $G$ que contém $S$ . Existem exemplos também em teoria da medida. Assim, como na Proposição 5.2, a interseção de uma família de subgrupos é um subgrupo, a interseção de uma família de subespaços vetoriais é um subespaço vetorial.

Deﬁnição 5.5.

Seja $X$ um conjunto, e $𝒞 \subset 𝒫 (X)$ uma família qualquer de subconjuntos de $X$ . Então a topologia

τ (𝒞) = \underset{𝒞 \subset τ_{X}}{\lor} τ_{X}

é a topologia gerada por $𝒞$ . Essa é a menor topologia de $X$ que contém a família $𝒞$ .

Deﬁnição 5.6.

Seja $X$ um conjunto qualquer, e $𝒞 \subset 𝒫 (X)$ uma família qualquer de subconjuntos de $X$ . Mesmo sem deﬁnir o que venha a ser uma base para a topologia (Deﬁnição 5.13), vamos deﬁnir o conjunto

ℬ (𝒞) = \{⋂_{A \in 𝒞^{'}} A| 𝒞^{'} \subset 𝒞, # 𝒞^{'} < \infty\},

e chamá-lo de base induzida pela família $𝒞$ . Aqui, usamos a convenção de que $⋂_{A \in \emptyset} A = X$ .

Observação 5.7. Na Deﬁnição 5.6, utilizamos a seguinte convenção:

\begin{array}{l} ⋃_{A \in \emptyset} A & = \emptyset \\ ⋂_{A \in \emptyset} A & = X . \end{array}

Esta convenção se torna mais natural se, considerando a relação de ordem $\subset$ em $𝒫 (X)$ , interpretarmos $\cup$ e $\cap$ como sendo operadores de supremo e ínﬁmo, assim como ﬁzemos na Observação 5.3. Desta forma, dado $ℱ \subset 𝒫 (X)$ ,

⋃_{A \in ℱ} A

é o menor subconjunto de $X$ que é maior que todos os conjuntos em $ℱ$ . Se $ℱ$ é vazio, então o menor subconjunto seria justamente $\emptyset$ . Da mesma forma,

⋂_{A \in ℱ} A

é o maior subconjunto de $X$ que é menor que todos os conjuntos em $ℱ$ . Se $ℱ = \emptyset$ , este conjunto é simplesmente o maior subconjunto de $X$ , que é o próprio $X$ .

Por um abuso de notação, quando $𝒞 = \{A_{λ}| λ \in Λ\}$ , por vezes escrevemos $τ (A_{λ}, λ \in Λ)$ no lugar de $τ (𝒞)$ . E quando $𝒞_{λ}, (λ \in Λ)$ é uma coleção de famílias de subconjuntos de $X$ , escrevemos $τ (𝒞_{λ}, λ \in Λ)$ ao invés de $τ (⋃_{λ \in Λ} 𝒞_{λ})$ . As seguintes propriedades da topologia gerada por uma família são consequência direta da deﬁnição. O leitor deve ﬁcar atento para a diferença entre

τ (𝒞_{λ}, λ \in Λ)

τ (𝒞_{λ}), λ \in Λ .

Proposição 5.8.

Sejam $𝒞$ e $𝒟$ famílias de subconjuntos de $X$ , e $τ_{X}$ uma topologia em $X$ . Então, valem as seguintes propriedades:

Todos os conjuntos em $𝒞$ são abertos na topologia gerada: $𝒞 \subset τ (𝒞)$ .
Se $𝒞 \subset 𝒟$ , então $τ (𝒞) \subset τ (𝒟)$ .
Temos que $𝒞 \subset τ_{X}$ se, e somente se, $τ (𝒞) \subset τ_{X}$ .

τ_{X}

é uma topologia, então

τ_{X} = τ (τ_{X})

. Em particular, vale que

τ (τ (𝒞)) = τ (𝒞) .

Se $𝒞 \subset τ_{X} \subset τ (𝒞)$ , então $τ_{X} = τ (𝒞)$ .
Se $𝒞 \subset 𝒟 \subset τ (𝒞)$ , então $τ (𝒞) = τ (𝒟)$ .
Se $ℰ = τ (𝒞) \cup τ (𝒟)$ , então $τ (ℰ) = τ (𝒞 \cup 𝒟)$ .
Seja $𝒞_{λ}, (λ \in Λ)$ uma coleção de famílias de subconjuntos de $X$ . Então,
$τ (τ (𝒞_{λ}), λ \in Λ) = τ (𝒞_{λ}, λ \in Λ) .$

Demonstração. Vamos mostrar apenas o item (8), que é mais difícil. O restante ﬁca como exercício. :-)

É evidente, pelo item (2), que

τ (⋃_{λ \in Λ} 𝒞_{λ}) \subset τ (⋃_{λ \in Λ} τ (𝒞_{λ})) .

No entanto, novamente pelo item (2), sabemos que para todo $γ \in Λ$ ,

τ (𝒞_{γ}) \subset τ (⋃_{λ \in Λ} 𝒞_{λ}) .

E portanto,

⋃_{λ \in Λ} τ (𝒞_{λ}) \subset τ (⋃_{λ \in Λ} 𝒞_{λ}) .

Agora, pelo item (5),

τ (⋃_{λ \in Λ} τ (𝒞_{λ})) = τ (⋃_{λ \in Λ} 𝒞_{λ}) .

□

5.2.1 Forma da Topologia Gerada

Qual é a forma de um aberto de $τ (𝒞)$ quando expresso em termos de $𝒞$ ? Obviamente que a topologia gerada por $𝒞$ deve conter todas as interseções ﬁnitas e todas as uniões de elementos de $𝒞$ . Mas isso nem sempre é suﬁciente. A Proposição 5.9 nos diz como podemos escrever os abertos da topologia gerada em termos de conjuntos da sub-base.

Proposição 5.9.

Seja $𝒞$ uma sub-base para um espaço topológico $(X, τ_{X})$ . Ou seja, $τ_{X} = τ (𝒞)$ . Considere a base induzida $ℬ = ℬ (𝒞)$ das interseções ﬁnitas de conjuntos de $𝒞$ . Então, todos os conjuntos da topologia são uniões de conjuntos de $ℬ$ :

τ_{X} = \{⋃_{A \in ℬ^{'}} A| ℬ^{'} \subset ℬ\} .

Demonstração. A topologia $τ (𝒞)$ necessariamente contém $ℬ$ . Assim,

𝒞 \subset ℬ \subset τ (𝒞) .

Considere então, a família $𝒰$ dada pelas uniões de elementos de $ℬ$ :

𝒰 = \{⋃_{A \in ℬ^{'}} A| ℬ^{'} \subset ℬ\} .

Novamente,

𝒞 \subset ℬ \subset 𝒰 \subset τ (𝒞) .

Para concluir que $τ_{X} = 𝒰$ , basta mostrar que $𝒰$ é uma topologia. Assim, como $τ_{X}$ é a menor que contém $𝒞$ , poderemos concluir que $τ_{X} = 𝒰$ . É imediato que

\emptyset, X \in 𝒰 .

Também é evidente pela própria deﬁnição de $𝒰$ , que $𝒰$ é fechado por uniões arbitrárias. Basta então veriﬁcar que se $A, B \in 𝒰$ , então $A \cap B \in 𝒰$ . Onde, para $ℬ_{A}, ℬ_{B} \subset ℬ$ adequados,

\begin{array}{l} A & = ⋃_{U \in ℬ_{A}} U \\ B & = ⋃_{V \in ℬ_{B}} V . \end{array}

Mas, neste caso,

A \cap B = ⋃_{W \in ℬ_{C}} W,

onde $ℬ_{C} = \{U \cap V| U \in ℬ_{A}, V \in ℬ_{B}\}$ . Agora, basta notar que $ℬ_{C} \subset ℬ$ , pois $ℬ$ é fechada por interseção ﬁnita. □

5.2.2 Sub-Base e Continuidade

Se temos uma aplicação $f : (X, τ_{X}) \to (Y, τ_{Y})$ , e uma sub-base $𝒞$ de $τ_{Y}$ , como podemos dizer, olhando para $f^{- 1} (𝒞)$ , se $f$ é ou não contínua. Um primeiro “chute” seria talvez dizer que basta que $f^{- 1} (𝒞) \subset τ_{X}$ . Obviamente que esta é uma condição necessária. A proposição seguinte é o elo que falta para mostrar que a condição $f^{- 1} (𝒞) \subset τ_{X}$ é equivalente à continuidade de $f$ .

Proposição 5.10.

Sejam $X$ e $Y$ dois conjuntos e $𝒞 \subset 𝒫 (Y)$ uma família de subconjuntos de $Y$ . Então,

τ (f^{- 1} (𝒞)) = f^{- 1} (τ (𝒞)) .

Demonstração. Vamos utilizar a seguinte notação:

\begin{array}{l} τ_{1} & = τ (f^{- 1} (𝒞)) \\ τ_{2} & = f^{- 1} (τ (𝒞)) . \end{array}

Por deﬁnição, $τ_{1}$ é uma topologia. É fácil ver (Exemplo 4.5) que $τ_{2}$ também é uma topologia. Como $f^{- 1} (𝒞) \subset τ_{2}$ , segue que

τ_{1} \subset τ_{2,}

pois $τ_{1}$ é a menor topologia com tal propriedade. Resta então mostrar que dado $A \in τ_{2}$ , teremos $A \in τ_{1}$ .

Pela Proposição 5.9, dado $A \in τ_{2}$ , basta mostrar que $A$ pode ser escrito como uma união arbitrária de interseções ﬁnitas de elementos de $f^{- 1} (𝒞)$ . De fato, $A = f^{- 1} (A^{'})$ , onde $A^{'} \in τ (𝒞)$ é uma união arbitrária de interseções ﬁnitas de elementos de $𝒞$ . Como $f^{- 1}$ comuta com as operações de união e interseção, temos a expressão desejada para $A$ , concluindo a demonstração. □

Conforme prometido, vamos utilizar a Proposição 5.10 para mostrar que para uma aplicação $f : (X, τ_{X}) \to (Y, τ (𝒞))$ ser contínua, basta que $f^{- 1} (𝒞) \subset τ_{X}$ .

Proposição 5.11.

Seja $f : (X, τ_{X}) \to (Y, τ_{Y})$ , onde $τ_{Y} = τ (𝒞)$ . Então, $f$ é contínua se, e somente se, $f^{- 1} (𝒞) \subset τ_{X}$ .

Demonstração. É evidente que a condição é necessária. Vamos mostrar que é suﬁciente. Pela Proposição 5.10, temos que

f^{- 1} (τ_{Y}) = τ (f^{- 1} (𝒞)) .

Mas a hipótese $f^{- 1} (𝒞) \subset τ_{X}$ implica que $τ (f^{- 1} (𝒞)) \subset τ_{X}$ . Ou seja,

f^{- 1} (τ_{Y}) = τ (f^{- 1} (𝒞)) \subset τ_{X} .

□

Observação 5.12. Frequentemente, demonstrações de que determinada função é contínua ﬁcam excessivamente complicadas porque o autor da demonstração refez o argumento das Proposições 5.10 e 5.11. Veja, por exemplo, a demonstração da Proposição 7.14.

5.2.3 Exercícios

5.2.1. Considere em $ℝ$ sua topologia usual, $τ$ , a topologia da continuidade inferior, $τ_{i}$ e a topologia da continuidade superior, $τ_{s}$ . Mostre que $f : X \to ℝ$ , onde $X$ é um espaço topológico qualquer, é contínua na topologia $τ$ se, e somente se, for contínua nas topologias $τ_{i}$ e $τ_{s}$ .

5.2.2. Seja $𝒮$ uma família de subconjuntos de $X$ que não cobre $X$ . Ou seja, $X \neq ⋃_{S \in 𝒳} S$ . Considere a topologia em $X$ gerada por $𝒮$ , e mostre que existe $x \in X$ tal que $𝒱_{} (x) = \{X\}$ .

5.2.3. Mostre que $f : X \to Y$ é aberta se, e somente se, é aberta em todo $x \in X$ .

5.2.4. Considere $f : (X, τ_{X}) \to (Y, τ_{Y})$ . Se $ℱ$ é uma família geradora da topologia $τ_{X}$ , então, $f$ é aberta se, e somente se, $f (ℱ) \subset τ_{Y}$ .

5.3 Bases

Dada uma família $𝒞$ de subconjuntos de um conjunto $X$ , a base induzida $ℬ = ℬ (𝒞)$ tinha uma propriedade interessante:

Todo aberto de $τ (ℬ)$ é uma união de elementos de $ℬ$ .

Cada família com essa propriedade é uma de base da topologia. Quando construímos a topologia dos espaços métricos, as bolas formavam uma base para a topologia (Proposição 3.14).

Deﬁnição 5.13.

Seja $(X, τ_{X})$ um espaço topológico. Uma família $ℬ \subset τ_{X}$ é uma base para a topologia $τ_{X}$ quando todo conjunto $A \in τ_{X}$ puder ser escrito como uma união de elementos de $ℬ$ . Aqui, seguimos a convenção de que $⋃_{A \in \emptyset} A = \emptyset$ ,

Como de costume, vamos ver outras maneiras de caracterizar o que vem a ser uma base para uma topologia $τ_{X}$ . Note que uma das condições da Deﬁnição 5.13 é que $ℬ \subset τ_{X}$ .

Proposição 5.14.

Seja $(X, τ_{X})$ um espaço topológico e $ℬ \subset 𝒫 (X)$ uma família de subconjuntos de $X$ . Então as seguintes aﬁrmações são equivalentes:

A família
$ρ = \{⋃_{A \in ℬ^{'}} A| ℬ^{'} \subset ℬ\}$

é uma topologia de $X$ . E além disso, $τ_{X} = ρ$ .
A família $ℬ$ é uma base para $τ_{X}$ .
Temos que $ℬ \subset τ_{X}$ , e para todo $x \in X$ e toda vizinhança $V$ de $x$ , existe $B \in ℬ$ tal que $x \in B \subset V$ .
Para todo $x \in X$ , o conjunto
$ℬ_{x} = \{A \in ℬ| x \in A\}$

é uma base de vizinhanças de $x$ (veja a Deﬁnição 4.10).
Para todo $A, B \in ℬ$ e $x \in A \cap B$ existe $C \in ℬ$ tal que $x \in C \subset A \cap B$ . E além disso, $τ_{X} = τ (ℬ)$ e $X = ⋃_{A \in ℬ} A$ .

Demonstração. _ (1) $\Rightarrow$ (2)

Pela deﬁnição de base, $ℬ$ é uma base para $ρ$ . Como

ℬ \subset ρ \subset τ (ℬ),

temos que $ρ = τ (ℬ) = τ_{X}$ .

_ (2) $\Rightarrow$ (3)

Se $ℬ$ é base para $τ_{X}$ , então $ℬ \subset τ_{X}$ . Seja $V \in 𝒱_{} (x)$ . Então, $A = \ddot{V}$ é aberto e $x \in A$ . Como o conjunto $A$ é da forma

A = ⋃_{B \in ℬ^{'}} B

para alguma sub-família $ℬ^{'} \subset ℬ$ , basta escolher $B \in ℬ^{'}$ tal que $x \in B$ , para que

x \in B \subset A \subset V .

_ (3) $\Rightarrow$ (4)

Evidentemente que $ℬ_{x} \subset 𝒱_{} (x)$ , já que a família é formada por conjuntos abertos que contém $x$ . Basta mostrar que para toda vizinhança $V$ de $x$ , existe $B \in ℬ_{x}$ tal que $B \subset V$ . Mas a existência de tal $B$ é justamente a hipótese do item (3).

_ (4) $\Rightarrow$ (5)

Se $A, B \in ℬ$ e $x \in A \cap B$ , então, por hipótese, $A$ e $B$ são vizinhanças de $x$ . Portanto, $A \cap B$ também é vizinhança de $x$ . Como $ℬ_{x}$ é uma base de vizinhanças de $x$ , então existe $C \in ℬ_{x}$ tal que

x \in C \subset A \cap B .

Precisamos então veriﬁcar que $ℬ$ gera $τ_{X}$ . Primeiramente, note que todo conjunto $U \in ℬ$ é aberto, pois se $x \in U$ , então $U \in ℬ_{x} \subset 𝒱_{} (x)$ . Ou seja, $U$ é vizinhança de todos os seus pontos. Assim,

τ (ℬ) \subset τ_{X} .

Por outro lado, todo aberto de $τ_{X}$ pode ser escrito como uma união de elementos de $ℬ$ , pois dado $V \in τ_{X}$ , para cada $x \in V$ existe $V_{x} \in ℬ_{x} \subset ℬ$ tal que $x \in V_{x} \subset V$ . Ou seja,

V = ⋃_{x \in V} V_{x} .

E portanto,

τ_{X} \subset τ (ℬ) .

É evidente que $X = ⋃_{A \in ℬ} A$ , pois nenhum dos $ℬ_{x}$ é vazio. (Note que acabamos provando que (4) $\Rightarrow$ (2).)

_ (5) $\Rightarrow$ (1)

Já sabemos que $\emptyset \in ρ$ . Pela hipótese de $X$ ser a união de todos os conjuntos em $ℬ$ , $X \in ρ$ . Por deﬁnição, $ρ$ é evidentemente fechada por união arbitrária. Resta mostrar que é também fechada por interseção ﬁnita. Para isso, basta notar que $A$ e $B$ são da forma

\begin{array}{l} A & = ⋃_{U \in ℬ_{A}} U \\ B & = ⋃_{V \in ℬ_{B}} V \end{array}

para $ℬ_{A}, ℬ_{B} \in ℬ$ adequados. Assim,

A \cap B = ⋃_{(U, V) \in ℬ_{A} \times ℬ_{B}} U \cap V,

sendo que, é fácil veriﬁcar que as hipóteses do item (5) implicam que cada $U \cap V$ é uma união de conjuntos em $ℬ$ . Portanto, $A \cap B \in ρ$ . □

Observação 5.15.

Dada uma família qualquer $𝒞 \subset 𝒫 (X)$ , a Proposição 5.9 mostra que $ℬ (𝒞)$ é uma base para $τ (𝒞)$ . Em particular, toda família $ℬ$ fechada por interseção ﬁnita é uma base para $τ (ℬ)$ . Esse fato pode ser veriﬁcado também pelo item (5) da Proposição 5.14. Esta condição não é, no entanto, necessária para que $ℬ$ seja uma base para $τ (ℬ)$ . As bolas, por exemplo, formam uma base para a topologia de um espaço métrico, mas não é necessariamente verdade que a interseção de duas bolas será uma bola.

Corolário 5.16. Seja $ℬ$ uma família de subconjuntos de $X$ , com $X = ⋃_{A \in ℬ} A$ . Para que $ℬ$ seja uma base de $τ (ℬ)$ é necessário e suﬁciente que para todo $A, B \in ℬ$ , $A \cap B$ possa ser escrito como união de elementos de $ℬ$ .

Demonstração. A condição é evidentemente necessária. Para ver que é suﬁciente, basta veriﬁcar as condições do item (5) da Proposição 5.14. Evidentemente que $ℬ$ gera $τ (ℬ)$ . O restante da demonstração ﬁca como exercício. □

5.3.1 Sub-Base e Convergência

A convergência de uma sequência $x_{n} \to x$ pode ser entendida como:

Para toda vizinhança $V$ de $x$ , por menor que seja, existe $N$ tal que

n \geq N \Rightarrow x_{n} \in V .

A expressão “por menor que seja” é um aposto, e é supérﬂua, mas traduz bem o fato de a convergência poder ser descrita em termos de bases, ou bases de vizinhanças (veja a Observação 4.13 e a Proposição 5.14). O fenômeno da convergência pode ser ainda mais fácil de ser veriﬁcado se utilizarmos uma sub-base ao invés de uma base.

Proposição 5.17. Seja $𝒮$ uma sub-base de um espaço topológico. Então, uma sequência $x_{n}$ converge para $x$ se, e somente se, para todo $V \in 𝒮$ , com $x \in V$ , existir $N = N (V)$ tal que

n \geq N \Rightarrow x_{n} \in V .

Demonstração. Seja $ℬ$ a base gerada por $𝒮$ . Basta mostrarmos que a condição garante que para todo $U \in ℬ$ , com $x \in U$ , existir $N = N (U)$ tal que

n \geq N \Rightarrow x_{n} \in U .

Note que ou $U = X$ (neste caso, basta tomar $N = 1$ ), ou $U = V_{1} \cap \dots \cap V_{n}$ , com $V_{j} \in 𝒮$ . Neste último caso,

N (U) = max (N (V_{1}), \dots, N (V_{n}))

satisfaz a condição desejada. □

5.3.2 Exercícios

5.3.1. Mostre que a família

ℬ = \{(a, b) \subset ℝ| a \in ℚ, b \notin ℚ\}

é uma base para a topologia usual de $ℝ$ .

5.3.2. Toda base é fechada por interseção ﬁnita não vazia? Demonstre que sim, ou dê um contra exemplo.

5.3.3. Complete a demonstração do Corolário 5.16.

5.4 Cardinalidade das Bases e Sub-Bases

Principalmente quando trabalhamos com sequências de elementos, ou mesmo sequências de conjuntos, a existência ou não de bases ou bases de vizinhanças que sejam enumeráveis torna-se uma questão importante.

Deﬁnição 5.18. Dizemos que um espaço topológico $X$ é segundo-enumerável quando possuir uma base enumerável. Se todo $x \in X$ possui uma base enumerável de vizinhanças, dizemos que $X$ é primeiro-enumerável.

Observação 5.19. A nomenclatura da Deﬁnição 5.18 é uma tradução direta da língua inglesa — ﬁrst countable e second countable —, e é muito ruim. Se um espaço topológico $X$ possui uma base enumerável, não seria melhor dizer que $X$ possui base enumerável? Da mesma forma, neste livro, vamos dizer que $x \in X$ possui base enumerável de vizinhanças. Ao invés de dizer primeiro-enumerável, vamos simplesmente dizer que todo ponto de $X$ possui base enumerável de vizinhanças.

Exemplo 5.20 (Espaço Métrico). Em um espaço métrico $X$ , um ponto qualquer possui uma base enumerável de vizinhanças. De fato, dado $x$ , as bolas de raio $\frac{1}{n}$ centradas em $x$ formam uma base de vizinhanças. Essa base de vizinhanças tem a propriedade de poder ser ordenada de forma decrescente. Ou seja,

B_{\frac{1}{n}} (x) \supset B_{\frac{1}{n + 1}} (x) .

Esta é a propriedade que nos permitiu estabelecer a equivalência entre continuidade com bolas e continuidade com sequências para aplicações entre espaços métricos. Veja a Proposição 2.10.

Na Deﬁnição 5.18, não mencionamos nada sobre a cardinalidade das sub-bases. A seguinte proposição explica porque.

Proposição 5.21. Em um espaço topológico $X$ com inﬁnitos abertos, existe uma base com cardinalidade $κ$ se, e somente se, existe uma sub-base com a mesma cardinalidade. Em particular, o espaço possui base enumerável se, e somente se possuir uma sub-base enumerável.

Demonstração. Como toda base é uma sub-base, basta mostrar que dada uma sub-base $𝒮$ , existe uma base $ℬ$ com a mesma cardinalidade que $𝒮$ . Primeiramente, é preciso notar que a cardinalidade de $𝒮$ não pode ser ﬁnita. Caso contrário, não existiriam inﬁnitos abertos na topologia.

Note que a família

ℬ_{n} = \{U_{1} \cap \dots \cap U_{n}| U_{1}, \dots, U_{n} \in 𝒮\}

tem a mesma cardinalidade que $𝒮$ (por quê?). Note também, que

ℬ = \{X\} \cup ⋃_{n = 1}^{\infty} ℬ_{n},

e portanto, $ℬ$ também tem a mesma cardinalidade que $𝒮$ (por quê?). □

Os espaços tais que todo ponto possui uma base enumerável de vizinhanças são semelhantes aos espaços métricos. Onde usaríamos sequências de bolas de raio $\frac{1}{n}$ , usamos a proposição abaixo. Um exemplo é a Proposição 5.23.

Proposição 5.22. Seja $X$ um espaço topológico e $x \in X$ um elemento qualquer. Se $x$ possui uma base enumerável inﬁnita de vizinhanças, $ℬ_{x}$ , então $x$ possui uma base de vizinhanças formada por conjuntos $B_{1}, B_{2}, \dots$ satisfazendo

B_{1} \supset B_{2} \supset B_{3} \supset \dots

Dizemos que $ℬ_{x}$ é uma base de vizinhanças encaixantes.

Demonstração. Seja $B_{1}^{'}, B_{2}^{'}, \dots$ uma enumeração dos elementos de $ℬ_{x}$ . Faça

B_{n} = ⋂_{j = 1}^{n} B_{j}^{'} .

Por ser interseção ﬁnita de vizinhanças de $x$ , cada $B_{n}$ é uma vizinhança de $x$ . E dada uma vizinhança qualquer de $x$ , $V$ , existe $n$ tal que $B_{n}^{'} \subset V$ . Ou seja,

B_{n} \subset B_{n}^{'} \subset V .

E portanto, os conjuntos $B_{n}$ formam uma base de vizinhanças de $x$ . □

É claro que se $x$ possuir uma base ﬁnita de vizinhanças, então $x$ possui uma base formada por apenas um elemento: a interseção de todos os elementos da base ﬁnita.

Em um espaço onde todo ponto possui base enumerável de vizinhanças, a topologia pode ser inteiramente descrita através de sequências e seus limites.

Proposição 5.23. Seja $X$ um espaço topológico, $x \in X$ , e $ℬ_{x} \subset 𝒱_{} (x)$ uma base enumerável de vizinhanças de $x$ . Então, a família $𝒱_{} (x)$ pode ser inteiramente determinada se soubermos quais são as sequências que convergem para $x$ .

Demonstração. Pela Proposição 5.22, podemos assumir que $ℬ_{x} = \{B_{1}, B_{2}, \dots\}$ , com $B_{n} \supset B_{n + 1}$ .

Vamos mostrar que $V$ é vizinhança de $x$ se, e somente se, para toda sequência convergente $x_{n} \to x$ , tivermos um $N$ tal que $n \geq N \Rightarrow x_{n} \in V$ . Se $V$ é vizinhança de $x$ , então, é evidente que para toda sequência $x_{n} \to x$ existe um tal $N$ . Por outro lado, se $V$ não é uma vizinhança de $x$ , então, para cada $n$ , existe $B_{n}$ tal que $B_{n} ∖ V \neq \emptyset$ . Tome $x_{n} \in B_{n} ∖ V$ . A sequência $x_{n}$ converge para $x$ (por quê?). No entanto, para a sequência $x_{n}$ , não existe o referido $N$ . □

Um exemplo de aplicação da enumerabilidade de uma base da topologia, é a demonstração da Proposição 9.28. Uma propriedade que está bastante relacionada é a separabilidade do espaço topológico.

Deﬁnição 5.24 (Espaço Separável). Um espaço topológico $X$ é separável quando houver um subconjunto enumerável denso. Ou seja, quando existir $S \subset X$ enumerável tal que $\bar{S} = X$ .

Uma das utilidades de se demonstrar que um espaço possui base enumerável, é poder concluir que este espaço é separável.

Proposição 5.25. Um espaço topológico com base enumerável é separável.

Demonstração. Seja $B_{1}, B_{2}, \dots$ uma base enumerável. Agora, para cada $B_{n}$ , escolha $x_{n} \in B_{n}$ . Então, o conjunto $S = \{x_{1}, x_{2}, \dots\}$ é denso. □

Por outro lado, uma das utilidades de se demonstrar que um espaço é separável, é, em alguns casos, poder concluir que este espaço possui base enumerável. É o que faremos na demonstração da Proposição 9.28.

Proposição 5.26. Um espaço métrico $(X, d)$ tem base enumerável se, e somente se, é separável.

Demonstração. Pela Proposição 5.25, basta mostrar que se $X$ for separável, então $X$ tem base enumerável. Seja $S \subset X$ um subconjunto enumerável denso. Basta, então, mostrar que

ℬ = \{B_{\frac{1}{n}} (x)| x \in S, n = 1, 2, \dots\}

é uma base para a topologia de $X$ .

Como $ℬ$ é uma família de abertos, basta mostrar que para todo $a \in X$ , dado $m \in ℕ *$ , existem $x \in S$ e $n \in ℕ *$ tais que

a \in B_{\frac{1}{n}} (x) \subset B_{\frac{1}{m}} (a) .

Pela densidade de $X$ , podemos escolher $x \in S$ tal que $d (x, a) < \frac{1}{2 m}$ . Assim, basta tomar $n = 2 m$ , pois além de termos $a \in B_{\frac{1}{n}} (x)$ , também temos que para todo $y \in B_{\frac{1}{n}} (x)$ ,

\begin{array}{l} d (y, a) & \leq d (y, x) + d (x, a) \\ < \frac{1}{2 m} + \frac{1}{2 m} = \frac{1}{m} . \end{array}

Ou seja, $B_{\frac{1}{n}} (x) \subset B_{\frac{1}{m}} (a)$ . □

5.4.1 Exercícios

5.4.1. Seja $𝒮$ uma família de subconjuntos de $X$ . Mostre que se $𝒮$ é uma família ﬁnita, então a topologia gerada por $𝒮$ também é ﬁnita.

5.4.2. Onde foi usado que $# 𝒮 = \infty$ na Proposição 5.21?

5.4.3. Dê um exemplo de um espaço topológico onde existe uma base ﬁnita de vizinhanças de um certo elemento $x$ , mas não existe uma base de vizinhanças composta por apenas um elemento.

5.4.4. Mostre que a sequência $x_{n}$ construida na demonstração da Proposição 5.23 de fato converge para $x$ .

Capítulo 5Construindo Topologias