Capítulo 7
Topologias
Derivadas de Outras Topologias
7.1 Topologia de um Sub-Espaço
Se temos um espaço topológico
e um subconjunto ,
então parece natural pensarmos na restrição da topologia
ao
subconjunto .
Mas isso é realmente natural? Vamos fazer algumas considerações.
Imagine que
é uma sequência (o ideal seria falar de “redes” — veja o Capítulo ??) que na topologia
converge para
. Neste caso, se fôssemos
“induzir” em uma
topologia a partir de
, sua topologia deveria
ser tal que para ,
Pensando em termos da operação de fecho, para um conjunto
, o conjunto
dos pontos de
que estão “próximos” — ou seja, no fecho — de
são, intuitivamente,
os pontos de
que estão em .
Ou seja, deveríamos ter que
Vendo do ponto de vista da continuidade, se
é uma aplicação
qualquer, e
é tal que ,
então podemos pensar na aplicação
e esperar que possamos induzir em
uma topologia tal que
é contínua se, e somente
se, o for. Poderíamos
também, dado , pensar
na continuidade de . Claro
que esperaríamos que se
é contínua em , então,
na topologia induzida,
deve ser contínua em .
Ou seja, se é
vizinhança de
em ,
deve ser
vizinhança de
em .
Dentre essas considerações, o menos natural é pensar em termos de abertos. E é
por isso que este livro é “de vários ângulos”. :-)
Entretanto, como nossa definição de espaço topológico é em termos de
abertos, com as ferramentas que temos até o momento, será mais fácil definir a
topologia de um subconjunto em termos de abertos. Felizmente, a definição com
abertos é extremamente simples.
Definição 7.1 (Topologia Induzida em um Subconjunto).
Seja um espaço
topológico e um
subconjunto de
qualquer. Então, o conjunto
é a topologia induzida por
em .
Notação. Na Definição 7.1, a notação
não é a interseção de
e ,
mas a família formada pela interseção dos elementos de
com o conjunto .
Este abuso de notação, em geral, não deve causar problemas de entendimento
e será usado sem ressalvas.
Vamos então verificar que a definição de topologia induzida em um
subconjunto satisfaz as propriedades discutidas no início do capítulo.
Proposição 7.2.
Seja um espaço
topológico e um subconjunto
qualquer de . Então a
topologia induzida em ,
,
satisfaz:
- Todo aberto
da topologia induzida é da forma
para algum aberto
da topologia de .
- Todo fechado
da topologia induzida é da forma
para algum fechado
da topologia de .
- Se ,
então
- Se ,
então
- Para ,
então
- Se é um espaço
topológico qualquer e é
uma aplicação tal que ,
então
é contínua se, e somente se,
é contínua. (Note que a diferença entre as aplicações
e
é apenas o contra-domínio das aplicações)
- Se é um espaço
topológico qualquer e
é uma aplicação contínua, então
é contínua.
Demonstração. _ Itens (1) e (2).
Imediato da definição de .
_ Item (3).
Imediato do item (1).
_ Item (4).
Este fato pode ser demonstrado de várias formas — de vários ângulos
;-). Vamos utilizar a Proposição 6.10, mas o leitor é motivado a demonstrar
diretamente da definição de fecho (Definição 6.1).
Pela Proposição 6.10 e pelo item (2),
(em que lugar da equação foi utilizado que
?)
_ Item (5).
Exercício.
_ Item (6)
Basta notar que .
_ Item (7)
Exercício. □
Observação 7.3. Para uma aplicação
e um subconjunto ,
sempre que falarmos de propriedades topológicas de
estaremos nos referindo à topologia .
De modo mais geral, a menos que se diga o contrário, consideraremos
dotado da topologia .
Observação 7.4. Note que se
é um aberto, então
Em particular, os abertos da topologia induzida são também abertos na
topologia original. Isso não vale em geral.
Da mesma forma, se
for fechado, os fechados da topologia induzida serão exatamente
os fechados da topologia original que estejam contidos em
.
(demonstre!)
Exemplo 7.5 (Topologia Induzida: ).
Considere a topologia no intervalo
induzida pela topologia usual dos números reais. Então, por exemplo, a família
é uma base de vizinhanças abertas para o ponto
.
Exemplo 7.6 (Espaço Métrico). Em um espaço métrico
, temos a
topologia , em
, induzida pela
métrica . Se
é um subconjunto
qualquer de ,
então, a princípio, temos duas maneiras canônicas de induzir uma topologia em
. Temos
, e temos também a
topologia induzida pela
restrição da métrica
ao conjunto :
|
|
Essas duas topologias coincidem. (por quê? dica: o que são as bolas na
métrica induzida?)
7.1.1 União Disjunta
Sejam
e
espaços topológicos disjuntos. O leitor não deverá ter problemas para se
convencer que é natural definir a topologia
|
|
em .
Note que .
Essa topologia é caracterizada pela propriedade
|
|
No Capítulo 8, estudaremos a existência de conjuntos que são
fechados e abertos ao mesmo tempo. Se em um espaço topológico
existe um subconjunto
próprio não vazio, ,
que é aberto e fechado ao mesmo tempo, então seu complemento,
também é aberto e fechado. Neste caso, os abertos de
são da
forma ,
onde e
. Dizemos
que
é desconexo (Definição 8.1).
7.1.2 Exercícios
7.1.1. Mostre que a família
da Definição 7.1 é de fato uma topologia.
7.1.2. Dê um exemplo de um espaço topológico
,
um subconjunto
e uma função
tais que
não é contínua, mas
é.
7.2 Topologias Inicial e Final
A topologia inicial é um dos conceitos mais importantes em topologia geral. Esta
seção deve ser estudada com muita atenção.
Se temos uma aplicação
de um conjunto
qualquer em um espaço topológico, a Proposição 5.10 mostra que
é uma
topologia em .
Não apenas isso, mas é também a menor topologia que torna
contínua. De
fato, é contínua
quando .
Mesmo quando estivermos tratando de uma família de aplicações
podemos falar da topologia mais fraca em
que torna
todas as
contínuas.
Definição 7.7.
Dada uma família de aplicações
a topologia
— a menor topologia tal que todas as aplicações
são
contínuas — é chamada de topologia (inicial) induzida pela família
.
Quando a família é composta por apenas uma aplicação
, a topologia inicial
é denotada por .
Da mesma forma, dada uma aplicação
de um espaço topológico
em um conjunto
qualquer, podemos nos perguntar qual seria a maior topologia que pode ser colocada em
de modo
que seja
contínua. O leitor deve se convencer de que a exigência “maior topologia tal que
seja contínua” faz
sentido. Afinal, se é
contínua, então será
contínua se a topologia de
for substituída por uma topologia mais fraca qualquer.
Definição 7.8.
Dada uma família de aplicações
a maior topologia em tal
que todas as aplicações
são contínuas é chamada de topologia final induzida pela família
.
Quando a família é composta por uma única aplicação
, denotamos a
topologia final por .
Daqui por diante, vamos omitir o conjunto de índices
quando conveniente, para simplificar a notação.
Observação 7.9. O caso em que o uso da topologia
final é mais útil, é quando se tem apenas uma função
. Para uma família
, se denotarmos por
a topologia final induzida
pela aplicação ,
então a topologia final induzida pela família toda será
Isso porque a inteseção de topologias é uma topologia.
Proposição 7.10.
Dada a aplicação , a
topologia final induzida por
é a família
Demonstração. Denote por
a família .
Evidentemente que ,
pois
é a maior família tal que .
Basta então mostrar que
é de fato uma topologia… deixemos isso como exercício ao leitor. :-) □
Exemplo 7.11 ().
A aplicação
é contínua quando consideramos as topologias usuais,
de
e
de
. A topologia inicial em
quando consideramos
a topologia usual em
é dada por
Ou, o que dá na mesma,
E qual é a topologia final de ?
7.2.1 Diagramas Comutativos
Quando temos uma família de aplicações cada uma com seu domínio e seu
contra-domínio, podemos representá-las em um diagrama. Por exemplo,
|
|
Dizemos que o diagrama comuta quando “diferentes caminhos” correspondem à
mesma aplicação. Se, por exemplo, o diagrama anterior comuta, então sabemos que
; ou
então, .
Vamos caracterizar as topologias inicial e final utilizando diagramas comutativos.
Proposição 7.12.
Dada a aplicação ,
a topologia inicial é
a única topologia
que torna
contínua e é tal que para todo diagrama comutativo
|
|
a continuidade de é
equivalente à continuidade de .
Demonstração. Primeiro vamos mostrar que para
, a continuidade de
é equivalente à
de . Primeiramente,
por definição,
torna contínua.
Se for contínua,
então é
contínua por ser a composição de duas aplicações contínuas. Por outro lado, supondo que
é contínua,
dado ,
é da
forma ,
com .
Assim,
|
|
Pela continuidade de ,
este conjunto é aberto de .
Ou seja, a imagem inversa de um aberto de
é aberto
de .
Portanto,
é contínua.
Falta mostrar que só existe uma topologia que satisfaz a condição da proposição.
Suponha que
e
ambas satisfaçam a condição do enunciado. Considere a seguinte o seguinte
diagrama comutativo.
|
|
Neste caso, como satisfaz
as condições do enunciado e
é contínua na topologia ,
temos que
é contínua. Mas a continuidade da identidade é equivalente a
Invertendo os papeis de
e ,
obtemos a unicidade:
□
Observação 7.13. Muitos autores começariam a demonstração
anterior pela unicidade. Na demonstração da unicidade, não foi preciso
utilizar a existência! Não foi preciso saber como é a “cara” da topologia
.
Optamos por considerar duas topologias quaisquer que satisfazem as
condições impostas e demonstrar que são necessariamente iguais.
Concluindo que se existe uma, então é única. Daqui por diante, quando
possível, começaremos esse tipo de demonstração pela unicidade.
A Proposição 7.12 admite a seguinte generalização.
Proposição 7.14.
Considere a família de aplicações
. A topologia
inicial em dada
pela família é a
única topologia
onde todas as
são contínuas, e para toda aplicação
vale que
|
|
Demonstração. _ Unicidade.
Seja
uma topologia que satisfaz as condições do enunciado, e
uma topologia
onde as
são contínuas. Considere a seguinte família de diagramas comutativos indexada
por .
|
|
Como satisfaz as
condições da proposição e
é contínua na topologia ,
então
é contínua. Ou seja,
Portanto, para uma topologia
que também satisfaz as condições da proposição, se invertermos os papeis
de
e ,
chegaremos à igualdade.
_ A topologia inicial possui as propriedades enunciadas.
Suponha que
seja a topologia inicial. Ou seja, a topologia gerada pela família
|
|
Pela Proposição 5.11,
□
A topologia final tem forma semelhante à inicial quando utilizamos diagramas
comutativos.
Proposição 7.15.
Dada a aplicação ,
a topologia final é
a única topologia,
que torna
contínua e é tal que para todo diagrama comutativo
|
|
a continuidade de é
equivalente à continuidade de .
Demonstração. Para mostrar a unicidade, considere as topologias
e
, e
suponha que ambas possuem as propriedades do enunciado. Então, o diagrama
comuta, e o fato de
ser contínua em ambas as topologias implica que
é
um homeomorfismo. Ou seja,
Vamos então mostrar que
satisfaz as condições da proposição. A parte não trivial é mostrar que a continuidade
de implica na
continuidade de .
Seja ,
então
|
|
é aberto de .
Pela definição de topologia final, temos que
é aberto
de . Ou
seja,
é contínua. □
7.2.2 Exemplos
Exemplo 7.16. Seja
um espaço normado. Faça
Vamos denotar por a
topologia da norma e por a
topologia inicial induzida em
por .
A aplicação
é contínua em .
Portanto,
No entanto, se
e , então
para
todo tal
que .
Portanto,
Por outro lado, as vizinhanças de
são as mesmas em ambas as topologias.
Fica demonstrado que denotar a topologia da norma por
foi
uma escolha ruim, pois a topologia da norma NÃO é a topologia inicial induzida
pela norma. :-p
Exemplo 7.17. Seja
um espaço métrico. Considere a família de funções
indexada por . Neste caso,
a topologia da métrica
é exatamente a topologia inicial induzida pela família
.
Exemplo 7.18. Seja o conjunto
das funções limitadas de
em . Para
cada ,
temos
A topologia inicial definida em
pela família
() é a
topologia da convergência ponto a ponto, onde
|
|
Veja a Seção 7.3.
Ainda podemos, para cada sequência
com
(ou
),
definir
|
|
etc. Podemos sempre obter topologias mais e mais fortes. No entanto, todas elas são
mais fracas que a topologia da norma do supremo, pois todas essas funções são contínuas
quando
é munido da norma
Se também considerarmos as sequências
,
temos uma topologia mais forte ainda. Podemos ainda fazer o mesmo para o
e
obtermos topologias cada vez mais fortes. No entanto, todas essas topologias
continuam sendo mais fracas que a topologia da norma do supremo, pois todas essas
funções são contínuas quando consideramos a norma do supremo em
.
7.2.3 Exercícios
7.2.1. Por que a
topologia inicial é definida como a mais fraca tal que a família de funções
é contínua, e não como a mais forte?
7.2.2. Por que
a topologia final é definida como a mais forte tal que a família de funções
é contínua, e não como a mais fraca?
7.2.3. Seja
uma família de aplicações. Mostre que
é, de fato, a menor topologia tal que todas as
são
contínuas.
7.2.4. Seja
uma família de aplicações. Mostre que
é a topologia mais forte tal que todas as
são
contínuas.
7.2.5. Complete a demonstração da Proposição 7.10.
7.2.6. Dê um exemplo de duas funções
e
tais
que
não é uma topologia.
7.2.7. Seja
a aplicação do Exemplo 7.11. Mostre que
7.2.8. Seja
a aplicação do Exemplo 7.11. Mostre que
7.2.9. Seja a aplicação
do Exemplo 7.11. Fixado ,
para cada ,
seja .
Mostre que
é uma base de vizinhanças de
na topologia final.
7.3 Topologia Produto
Quando temos dois espaços métricos,
e
, de que forma podemos
gerar uma métrica em ?
Se e
forem o
conjunto dos números reais com a métrica usual (euclidiana), o que poderia ser a métrica
em ?
Poderia ser a métrica euclidiana (Exemplo 1.10), ou a métrica do máximo
(Exemplo 1.11), ou então a métrica da soma. Pelo exercício ??, todas
essas métricas são topologicamente equivalentes e possuem a seguinte
propriedade
Para uma sequência
e ,
temos que
|
|
Esta propriedade é facilmente verificada para a métrica do máximo e, pela
equivalência topológica, vale para todas as três. A topologia produto que
queremos definir — lembre-se que não temos uma métrica — será exatamente a
topologia da “convergência/continuidade coordenada a coordenada”.
7.3.1 Entre dois Espaços
Inspirados pelo fato de que na métrica do máximo (Exemplo 1.11) as bolas são
na verdade quadrados, vamos definir o produto de dois espaços topológicos como
sendo o espaço onde a base da topologia serão os “retângulos”.
Definição 7.19 (Topologia do Produto de dois Espaços).
Sejam
e
dois espaços topológicos. Definimos o espaço
produto como sendo o espaço topológico
,
onde
é gerada pelos conjuntos da forma ,
onde
e .
A topologia
é chamada de topologia produto. Por um abuso de notação, escrevemos
para designar a topologia produto. Quando
queremos ser menos ambíguos, escrevemos
.
As projeções canônicas em
e
e
exercem papel fundamental no estudo das topologias produto.
Observação 7.20.
Na Definição 7.19, poderíamos ter dito que a
topologia produto é gerada pelos conjuntos da forma
e ,
onde
e .
No entanto, os conjuntos da forma ,
além de geradores são também uma base da topologia. Isso está de acordo
com a analogia com a métrica do máximo, onde as bolas — que são uma
base para a topologia — são os “quadrados.” No caso da topologia produto,
não temos “quadrados,” temos “retângulos.”
Proposição 7.21.
Sejam e
dois espaços topológicos
e uma topologia
qualquer no conjunto .
As seguintes afirmações são equivalentes.
- A topologia
é a topologia produto. Ou seja,
- Os conjuntos da forma ,
onde e
formam uma
base de .
- Os conjuntos da forma
e ,
onde e
formam uma
sub-base de .
- A topologia é a
menor topologia em
tal que as projeções canônicas são contínuas. Ou seja, é a topologia
inicial induzida pelas projeções.
- Toda aplicação
com domínio em um espaço topológico
qualquer é contínua
se, e somente se,
e
forem contínuas.
Demonstração. _
Imediato da definição de topologia produto
e da Observação 5.15. Basta notar que
.
_
As projeções são contínuas se, e somente se, para todo
e ,
e .
Assim, a menor topologia em
que torna as projeções contínuas é a
topologia gerada pelos conjuntos da forma
e ,
para
e .
_
É um caso particular da Proposição 7.14. □
Observação 7.22. Se para
escrevermos
então
e .
O item (5) da proposição diz que na topologia produto,
é contínua se,
e somente se,
e
são contínuas.
Observação 7.23. Seja .
O item (5) da Proposição 7.21 pode sugerir que a continuidade de
no ponto
seja equivalente à continuidade de
e .
No entanto, a continuidade dessas duas seções de
é uma condição mais fraca que a continuidade de
.
Se é contínua
em , isso significa que se
“nos aproximarmos” de
na “vertical”, o valor de
se aproxima de . A
continuidade de
em corresponde à
continuidade de
na “horizontal”. No entanto, isso não garante nada sobre o comportamento de
quando “nos
aproximamos” de
pela “diagonal”, ou mesmo por um caminho em “espiral”. Um exemplo concreto é a
aplicação ,
dada por
|
|
Neste caso, .
No entanto, .
Observação 7.24. Para a topologia produto, também vale que
|
| (7.1) |
No entanto, como as sequências convergentes não determinam a topologia,
não se pode afirmar que a condição acima determina a topologia produto.
Se ao invés de sequências, utilizássemos o conceito de redes
— desenvolvido no Capítulo ?? —, a relação da equação 7.1
caracterizaria totalmente a topologia. Com redes no lugar de sequências,
será contínua se, e somente se, para toda rede
,
tivermos
|
|
7.3.2 Produto Finito
As considerações que foram feitas para o produto de dois espaços topológicos
podem ser facilmente estendidas para definir e caracterizar o produto de uma
quantidade finita de espaços topológicos.
Definição 7.25.
Dada uma família de espaços topológicos
, a topologia produto é
a menor topologia de
onde as projeções em cada coordenada,
|
|
são contínuas. O espaço (topológico) produto
, é o
conjunto ,
dotado da topologia produto.
O leitor fica encarregado de enunciar e demonstrar uma proposição análoga a
7.21.
7.3.3 Produto Infinito
Se temos um espaço topológico
para cada ,
pela experiência com o produto de uma família finita de espaços
topológicos podemos logo imaginar duas topologias que poderíamos
chamar de topologia produto. Uma delas, seria a topologia em
gerada pela família
dos conjuntos da forma ,
onde .
Se estivéssemos falando de espaços métricos, seria como definir a métrica do
supremo (veja o Exemplo ??). Esta topologia é bastante geométrica e intuitiva. No
entanto, não é esta a topologia que chamamos de topologia produto da família
(). A
topologia produto é um pouco mais fraca, possui propriedades importantes (por
exemplo, o Teorema 9.41) e é, em geral, mais fácil de se trabalhar.
Definição 7.26. Dada uma coleção qualquer de espaços topológicos
, a topologia produto é
a menor topologia de
onde as projeções em cada coordenada,
|
|
são contínuas. O espaço (topológico) produto
, é o
conjunto ,
dotado da topologia produto.
Desta forma, a topologia produto é a topologia mais fraca tal que as projeções
canônicas
são contínuas. Novamente, o leitor fica encarregado de enunciar e demonstrar uma
proposição análoga a 7.21.
Proposição 7.27. Dada uma coleção qualquer de espaços topológicos
,
seja
o espaço produto munido da topologia produto. Então,
é contínua se, e somente se,
é contínua para todo .
Demonstração. Basta aplicar a Proposição 7.14. □
Exemplo 7.28. Considere o conjunto
e as
seguintes normas
A topologia da norma
é a topologia produto. De fato, nesta norma, a bola centrada em
, de
raio
é igual a
|
|
onde
é tal que .
A topologia da norma
é mais forte que a topologia produto. Neste caso, a bola centrada em
, de
raio
é igual a
que pode não é aberto quando
para uma quantidade infinita de índices
.
Proposição 7.29. Sejam
espaços topológicos, e
as projeções canônicas
Então, cada
é uma aplicação aberta.
Demonstração. De fato, vamos mostrar que
é uma aplicação
aberta quando o produto
é dotado da topologia cuja base são os conjuntos da forma
onde .
Note que esta topologia é mais forte que a topologia produto, e portanto, se
for uma
aplicação aberta nesta topologia, será aberta na topologia produto. A imagem
por
de é
,
que é aberto. Como a imagem de uniões é a união das
imagens, e os abertos são uniões de elementos da base, segue que
é
uma aplicação aberta. □
Proposição 7.30. Sejam
espaços topológicos,
o espaço produto e
as projeções canônicas
Então, escolhendo ,
para cada ,
o conjunto da forma
|
|
é homeomorfo a .
Demonstração. A topologia de
é gerada pela família
onde , e
é um aberto de
. Mas exceto quando
, esses conjuntos ou
são vazios, ou iguais a .
Assim, a topologia de
é gerada pela família
onde é
um aberto de .
Essa família é uma topologia. Portanto, esses são exatamente os abertos de
. Isso implica que a
bijeção contínua
é também uma aplicação aberta. De fato,
|
|
Ou seja,
é um homeomorfismo. □
Exemplo 7.31 (Representação Decimal). Considere o conjunto
dos
dígitos de
a . O
espaço
pode ser utilizado para representar números reais no intervalo
. Enxergamos
um elemento
como sendo o número real cuja representação decimal é
.
Formalmente, a representação é feita pela função
|
|
Note, no entanto, que a aplicação
não é uma
bijeção. Apesar de
ser sobrejetiva, existem números que possuem duas representações distintas. Por
exemplo,
Na topologia produto, uma sequência
converge
para , quando
para todo ,
. No entanto,
como
é discreto, isso significa que a partir de um certo
,
Em outras palavras, para todo ,
existe
tal que
Assim, na topologia produto,
converge para
quando para todo , a
partir de um certo ,
os primeiros termos
de coincidem com os
primeiros termos
de . Em particular,
a aplicação é
contínua, pois se
converge para ,
então, para todo ,
existe tal que os
primeiros termos
de coincidem
com os de , para
todo . E isso
implica que .
É comum utilizarmos o espaço ,
ao invés de .
Neste caso, trabalhamos com a representação binária dos elementos de
.
Exemplo 7.32 (Espaço de Funções: convergência pontual). Sejam
um conjunto
qualquer, e
um espaço topológico. Podemos identificar as funções
com
os elementos do conjunto
onde é uma
cópia do espaço .
Se dotarmos
da topologia produto, temos uma noção de convergência no espaço das funções
de em
. Nesta topologia,
uma vizinhança
de são as
funções
que para um certo número finito de pontos (coordenadas)
,
e
diferem “pouco”. Para que
pertença a esta vizinhança
, não faz diferença que
valores assume em pontos
diferentes de . Para ser
preciso, uma vizinhança é
um conjunto que contém
para determinados , e
determinadas vizinhanças .
Pela Proposição 5.17, uma sequência
converge para
nesta topologia, exatamente
quando, para todo ,
.
Por isso, esta topologia no espaço das funções de
a
é
chamada de topologia da convergência pontual, ou topologia da convergência ponto
a ponto.
7.3.4 Exercícios
7.3.1.
Seja
uma aplicação qualquer entre os espaços topológicos
e
. O
gráfico de
é o conjunto
|
|
Mostre que quando
é contínua e
é um espaço métrico, o seu gráfico é um subconjunto fechado de
. (Veja
também a definição de espaço de Hausdorff: 9.29)
7.3.2. Encontre uma função contínua
cujo gráfico não seja um subconjunto fechado de
.
7.3.3.
Mostre que o conjunto
|
|
é fechado em .
7.3.4.
Mostre que, apesar de
|
|
ser um conjunto fechado pelo exercício 7.3.3, a projeção de
na primeira (e também na segunda) coordenada não é um conjunto
fechado.
7.3.5. Explique o que representa o conjunto
na Proposição 7.30.
7.3.6. Explique porque, na demonstração da Proposição 7.30,
ou é vazio ou é
quando .
7.3.7. Por que no Exemplo 7.31 pudemos afirmar que
é
contínua baseado apenas no fato de
7.3.8. Seja
() uma família de
espaços topológicos e
um subconjunto de índices. Vamos denotar por
|
|
Mostre que a aplicação
|
|
é contínua e aberta.
7.3.9. No mesmo contexto do Exercício 7.3.8, suponha que
é uma
partição de .
Mostre que a aplicação
|
|
é um homeomorfismo.
7.4 Topologia Quociente
Quando temos um conjunto qualquer ,
é comum querermos identificar uma classe de pontos de
como
se fossem um só. Por exemplo, o círculo pode ser visto como o intervalo
com os
pontos e
identificados. A ideia é
particionar em classes de
equivalência. O intervalo
com os pontos
e
identificados corresponde à partição
O círculo também pode ser visto como
com os
pontos e
identificados
sempre que .
Neste caso,
é particionado pela família
onde .
Ou seja, tomamos uma família
de subconjuntos
disjuntos, tais que
Existe uma projeção natural
onde é o único
elemento tal que
. Assim, podemos
colocar em a topologia
final induzida por .
7.4.1 Relação de Equivalência
Estamos preocupados em “particionar” um conjunto
e pensar no
conjunto
formado pelos elementos da partição escolhida. Uma maneira muito comum de se escolher uma
partição de
é através de uma relação de equivalência. Não vamos entrar
em detalhes quanto às propriedades das relações de equivalência,
mas de fato, definir uma relação de equivalência no conjunto
equivale a particioná-lo.
Definição 7.33. Uma relação
em um conjunto é simplesmente
um subconjunto de .
Usualmente escrevemos
ao invés de dizer que
pertence à relação .
Definição 7.34. Uma relação (binária)
definida em
um conjunto
é uma relação de equivalência se satisfizer, para todo
,
- .
- .
- .
Definir uma relação de equivalência em
é
equivalente a particioná-lo, pois dada uma relação de equivalência podemos particionar
em
classes de equivalência, ou seja, nos conjuntos
Do mesmo modo, dada uma partição
de
,
podemos definir a relação de equivalência
|
|
Notação. Dada uma relação de equivalência
em
, denotamos por
o conjunto das classes
de equivalência de . A
projeção natural de
em é
a aplicação dada por
Ao identificarmos, por exemplo, os pontos
e
do
intervalo
para formar o círculo, chamando esse ponto identificado de
, a
topologia que esperamos deve ser tal que, uma sequência converge para o ponto
sempre que se
aproximar do conjunto .
Dessa forma, uma sequência que se aproxima de
é uma sequência
que se aproxima de ,
ou de ,
ou que “oscila” entre esses dois pontos. O que queremos, é que cada vizinhança de
seja união de uma
vizinhança de e
uma vizinhança de .
Ou seja, queremos que a projeção canônica,
seja
contínua. Mas também, não esperamos que uma sequência que nem mesmo se
aproxima de
ou de
seja considerada uma sequência que se aproxima de
.
Queremos que a topologia seja a mais forte possível com esta propriedade.
Definição 7.35 (Topologia Quociente). Quando
é um espaço topológico e
uma relação de equivalência definida sobre
,
a topologia quociente em
é a topologia final induzida pela projeção natural.
Seja um conjunto
e uma relação de
equivalência em .
Suponha que a aplicação
seja tal que .
Neste caso, podemos definir
Note que o seguinte diagrama
é comutativo. Assim, pela Proposição 7.15, sabemos que a topologia
quociente fará com que uma eventual continuidade da aplicação
seja equivalente à
continuidade de .
Construções com “quocientes” são muito comuns, por exemplo, em álgebra,
onde quocientamos grupos por subgrupos, anéis por ideais, espaços vetoriais por
subespaços vetoriais e assim por diante. Em muitos casos, essas estruturas
algébricas são também dotadas de topologia. Mais a diante, no Capítulo ??,
por exemplo, veremos como o estudo da topologia pode facilitar a compreensão
desses espaços.
7.4.2 Exemplos
Exemplo 7.36 (O Círculo Unitário ).
O círculo unitário
pode ser visto, dentre outras maneiras, como o subconjunto dos números complexos de valor
absoluto , ou
como o conjunto ,
onde
Costumamos denotar este quociente por
.
Neste caso, podemos pensar, por exemplo, nas seguintes topologias em
:
- A topologia induzida em
quando visto como um subconjunto de
.
- A topologia final induzida pela aplicação
- A topologia quociente dada pela identificação usual entre
e
.
As topologias dos itens (2) e (3) são de fato a mesma topologia. Isso
porque a relação de equivalência do item (3) é dada exatamente por
fazendo com que o diagrama
seja comutativo. Onde
é justamente a bijeção que usualmente identifica
e
. As
aplicações
e
são contínuas respectivamente na topologia final induzida por
e na topologia final (topologia quociente) induzida por
. Pela
caracterização de topologia final dada pela Proposição 7.15, isso implica que tanto
quanto
são contínuas.
Ou seja,
é um homeomorfismo.
Quanto à equivalência entre os itens (1) e (3), considere
com a topologia induzida. Sabemos que, como
é contínua (Exercício
7.4.1), então
também é. Para concluir que todas as três topologias são iguais, precisamos mostrar que
é contínua
quando
é dotado da topologia induzida. Isso será feito mais adiante. Será consequência
direta da Proposição 9.34.
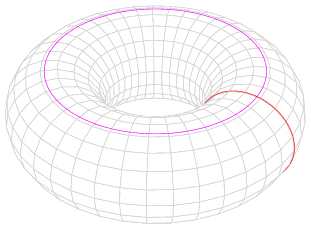
Exemplo 7.37 (O Toro ).
A forma da Figura 7.1 é o chamado toro bidimensional:
.
Uma generalização é o toro -dimensional:
.
O círculo é o toro unidimensional.
O toro -dimensional
pode ser definido como o espaço produto
de
cópias do
círculo unitário (Figura 7.1), mas também pode ser visto como o espaço quociente
, onde a
relação
é dada por
Costumamos denotar este quociente por
.
Assumindo que
é munido da topologia do item (2) do Exemplo 7.36, podemos colocar no
toro a topologia produto ou a topologia quociente. Novamente, ambas as
topologias irão coincidir. Para ver isso, basta considerar o diagrama comutativo
|
|
onde
é dado por
|
|
Note que é a
identificação usual entre
e .
7.4.3 Exercícios
7.4.1. Mostre que,
onde , é contínua
nas topologias usuais de
e .
7.4.2. Suponha que a projeção canônica
seja uma aplicação
aberta e que
é uma bijeção. Então,
|
|
é homeomorfismo
se, e somente se,
é aberta e fechada.
7.4.3. Dê um exemplo de uma relação de equivalência
em
tal que a projeção canônica
não é aberta.
7.5 Topologias das Sequências Convergentes
Esta seção pode (e deve!) ser omitida. É apenas uma divagação sobre
convergência de sequências. Ao fazer analogia com os espaços métricos, o
estudante frequentemente se pergunta porque é que nem sempre se pode usar
sequências para determinar as propriedades topológicas de um espaço.
Se temos um conjunto
e uma topologia
sobre ,
sabemos exatamente quais são e quais não são as sequências convergentes. No
entanto, conhecer as sequências convergentes não garante que conheçamos a
topologia. De fato, duas topologias distintas podem ter exatamente as mesmas
sequências convergentes, convergindo para os mesmos limites.
Exemplo 7.38 (Topologia Coenumerável). Seja
um
conjunto não enumerável, e
As sequências convergentes em
são aquelas que a partir de um certo índice se tornam constantes. Ou seja, as
sequências constantes a menos de um número finito de termos.
Considere agora
dada por
|
|
Fica como exercício mostrar que
é de fato uma topologia. Evidentemente que as sequências constantes a menos de um
número finito de termos convergem nesta e em qualquer outra topologia. Considere então a
sequência .
Suponha que
O conjunto
é vizinhança aberta de
em . A convergência
de implica que
para um certo ,
Mas só
está em se
. Ou seja,
é constante a menos,
possivelmente, de .
Pergunta: porque sabemos que ?
Dado um espaço topológico ,
podemos indagar se existe uma topologia
que é a menor onde as sequências convergentes são as mesmas que de
.
Também podemos nos perguntar se não existe a maior topologia
com esta mesma
propriedade. Se existir,
será a interseção da família de todas as topologias
() tais que
para todo ,
Vamos definir
como sendo
Evidentemente que como ,
então toda vizinhança de
em também é uma
vizinhança em .
Portanto,
No entanto, a implicação contrária pode não ser verdadeira. Ou seja, é possível que,
para a topologia ,
não tenhamos
Para um exemplo, veja:
http://math.stackexchange.com/questions/395980/topology-_for-_convergent-_sequences Para compreender o exemplo é
necessário conhecer um conceito mais avançado chamado “ultrafiltro”. Para nossos
propósitos, basta dizer que o exemplo se trata de uma família de topologias
no conjunto
tais que
equivale à
existência de
tal que
No entanto, em ,
equivale à
existência de
tal que
|
|
Ou seja, sempre
que “sai” de qualquer
subconjunto finito de .
Por outro lado, vamos definir a topologia
|
|
É evidente que é uma
topologia e é mais forte que .
O leitor é convidado a demonstrar essa afirmação.
Como ,
sabemos que
Por outro lado, pela definição de
,
sabemos que
Ou seja, sempre existe a topologia mais forte determinada
pela família de sequências convergentes de uma toplogia
dada. Em outras
palavras, denotando por
a família de topologias
temos que
é tal que , mas
pode ocorrer que
não pertença a .
7.5.1 Exercícios
7.5.1. Mostre que a topologia coenumerável
(
no Exemplo 7.38) é de fato uma topologia.
7.5.2. Por que sabemos que
no Exemplo 7.38?
7.5.3. Demonstre a implicação da Equação 7.2 na página 315.