4 Motivacao e Deﬁnicoes

Capítulo 4
Motivação e Deﬁnições

4.1 Motivação

Esta seção não é formal. Nosso propósito aqui é apenas dar motivação para as deﬁnições e propriedades que serão estudadas nas seções seguintes. Se o leitor não se sentir confortável com as divagações desta seção, pode omití-la sem problemas.

Nossa motivação é obviamente o estudo que acabamos de fazer de espaços métricos. Devidamente motivados pelo estudo feito na primeira parte do livro, vamos abstrair o que seria a essência dos fenômenos de convergência e continuidade. Uma alternativa seria associar ao espaço $X$ em questão uma estrutura que identiﬁcasse, para cada um dos pontos $x \in X$ , quais são e quais não são as sequências que convergem para $x$ . Uma deﬁciência desta abordagem está na dependência para com o conjunto dos números naturais, que indexam as tais sequências. Futuramente, veremos que uma solução alternativa é o uso de redes em substituição ao de sequência. Esta abordagem será feita no Capítulo ??.

Outra maneira seria associar a $X$ uma estrutura que indicasse, quais são os conjuntos que formam as “vizinhanças” de cada ponto de $X$ . A família das vizinhanças de $x \in X$ , denotadas por $𝒱_{} (x)$ , indica do que é que $x$ está “próximo” e do que é que está “afastado”. O ponto $x$ está próximo de um conjunto $B \in X$ quando para todo $V \in 𝒱_{} (x)$ , tivermos $B \cap V \neq \emptyset$ . A palavra “próximo” está entre aspas porque esse não é o termo matemático utilizado. Dizemos que $x$ está no fecho de $B$ (Deﬁnição 6.1), ou que é um ponto de aderência de $B$ .

As famílias $𝒱_{} (x)$ deveriam satisfazer as propriedades listadas na Proposição 3.4. O item (1) não gera grandes polêmicas. Para que um conjunto esteja próximo do ponto, tem que interceptar todas as suas vizinhanças, portanto, acrescentar conjuntos maiores não modiﬁcaria a “convergência”. Talvez o nome “vizinhança” não seja realmente uma boa escolha, já que sugere que sejam conjuntos pequenos. Mas ao contrário disso, as vizinhanças são conjuntos que são grandes o suﬁciente para conter uma bola, no caso dos espaços métricos. Quando dizemos

[…] para todas as vizinhanças […],

geralmente estamos omitindo uma referência a uma expressão do tipo “por menores que sejam”. Em uma conversa, se quiséssemos enfatizar, diríamos

[…] para todas as vizinhanças, por menores que sejam […]

Esse tipo de argumento poderia ser restrito às vizinhanças “pequenas”, e é por isso que existe a noção de base de vizinhanças de um ponto (Veja a Deﬁnição 3.7 e a Proposição 3.8). Assim, o item (1) se presta mesmo a maximizar a família $𝒱_{} (x)$ de modo que o fenômeno de convergência não seja alterado.

Do ponto de vista do fenômeno de convergência, o item (2) também serve ao mesmo propósito de maximizar a família $𝒱_{} (x)$ . Isso porque, se para $U, V \in 𝒱_{} (x)$ , existem $N_{U}, N_{V} \in ℕ$ tais que

\begin{array}{l} n \geq N_{U} & \Rightarrow x_{n} \in U \\ n \geq N_{V} & \Rightarrow x_{n} \in V, \end{array}

então, fazendo $N_{U \cap V} = max {N_{U}, N_{V}}$ ,

n \geq N_{U \cap V} \Rightarrow x_{n} \in U \cap V .

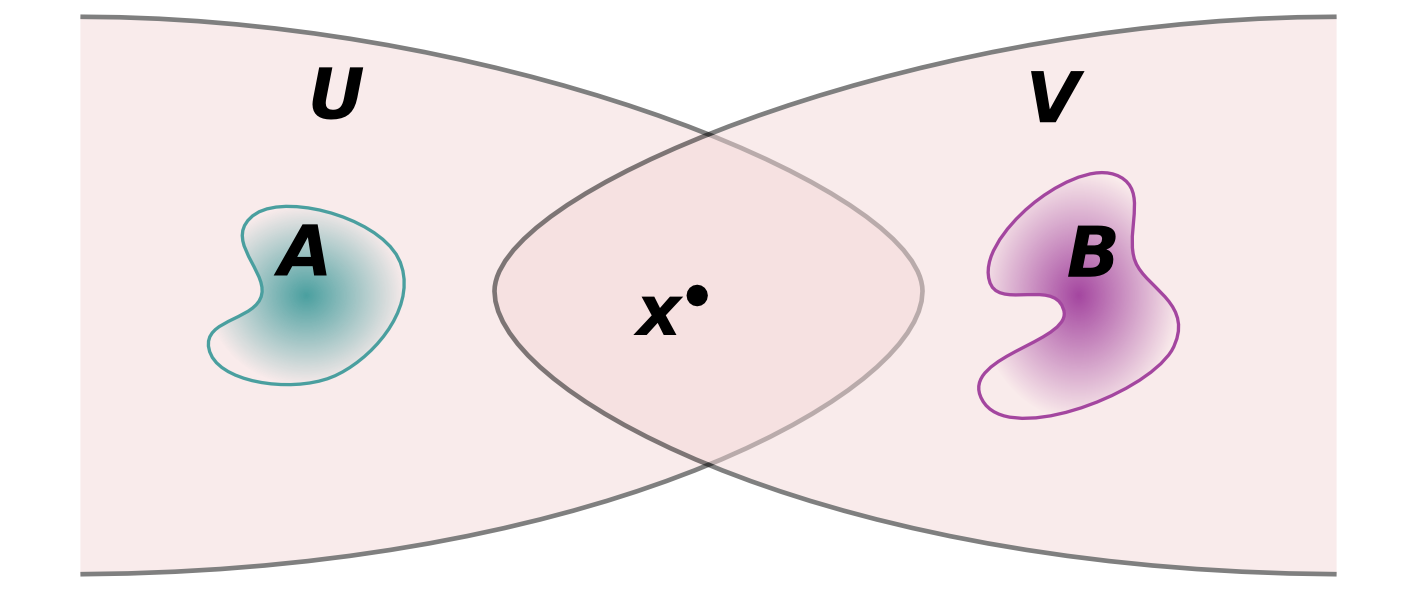
Assim, se $U$ e $V$ são vizinhanças de $x$ , levar ou não em consideração o conjunto $U \cap V$ como sendo vizinhança de $x$ não afetaria o fenômeno de convergência. O que não é convergente continua não convergente, e o que é convergente permanece convergente. Já do ponto de vista da idéia de “proximidade”, a condição do item (2) garante que se dois conjuntos $A$ e $B$ estão longe de $x$ , então a união $A \cup B$ também está longe de $x$ . Veja a Figura 4.1. Em espaços métricos, todos os pontos estão distantes uns dos outros. Assim, nenhum conjunto ﬁnito está “próximo” de $x$ , a menos que o contenha. Por outro lado, uma sequência inﬁnita de pontos $x_{n}$ distintos de $x$ pode convergir para $x$ . No caso de espaços topológicos gerais, é possível que uma família inﬁnita de conjuntos $A_{n}$ “afastados” de $x$ seja tal que $⋃ A_{n}$ esteja “próximo” de $x$ , mas as uniões ﬁnitas estarão sempre “afastados” de $x$ .

Figura 4.1: O conjunto

A

está “afastado” de

x

por não interceptar a vizinhança

V

. Da mesma forma,

B

também está “afastado”de

x

. Então, a união

A \cup B

também está “afastada” de

x

, pois

U \cap V

é vizinhança de

x

O item mais difícil de aceitar da Proposição 3.4, é o item (3). Como já mencionamos anteriormente (Observação 3.5), este item serve para garantir que se $x_{m}^{n} \to x_{n}$ e para alguma vizinhança $V \in 𝒱_{} (x)$ for verdade que $x_{m}^{n} \notin V$ , então não é possível acontecer que $x_{n} \to x$ . É equivalente a dizer que os abertos que contém $x \in X$ formam uma base de vizinhanças de $X$ . É o que garante que se conhecermos os abertos, conheceremos toda a topologia.

Uma outra interpretação para o item (3) pode ser vista através da Figura 4.2. Suponha que $A \subset X$ é um conjunto “afastado” de $x$ , e $L \subset X$ é tal que $A$ está próximo de todos os pontos de $L$ . Então, $L$ também é um conjunto “afastado” de $x$ . De fato, se toda vizinhança $V$ de $x$ intersectar $L$ , a condição do item (3) garante a existência de uma vizinhança aberta de $x$ $U$ contida em $V$ . Esta vizinhança $U$ intersecta $L$ , mas por ser um conjunto aberto, $U$ é também vizinhança dos pontos $y \in U \cap L$ . Como estes pontos estão “próximos” de $A$ , temos que $U$ e, a fortiori, $V$ intersectam $A$ . Ou seja, toda vizinhança de $x$ intersecta $A$ e portanto, $A$ está “próximo” de $x$ . Mais adiante, veremos que a condição imposta ao conjunto $L$ é o mesmo que dizer que $L$ está no fecho (Deﬁnição 6.1) de $A$ . E a condição do item (3) equivale a dizer que a operação de fecho é idempotente. (veja o item (4) da Proposição 6.4)

Figura 4.2: Todos os pontos de

L

estão “próximos” de

A

, que por sua vez, está “afastado” de

x

. Então

L

também está afastado de

x

, pois se existisse

y \in L \cap U

, então

U

seria vizinhança de

y

e, por hipótese, intersectaria

A

Já que nossa tentativa de deﬁnir “topologia” de um modo abstrato utilizando o conceito de vizinhança passa necessariamente pela idéia de conjunto aberto, e os conjuntos abertos por si só determinam o que vem a ser uma vizinhança de $x$ (é um conjunto que contém um aberto que contém $x$ — Proposição 3.12), a opção que vamos adotar, ao menos por enquanto, é a de deﬁnir a topologia especiﬁcando quais seriam os conjuntos abertos. Para um conjunto $X$ , escolhemos $τ_{X} \subset 𝒫 (X)$ de modo que $τ_{X}$ tenha as propriedades listadas na Proposição 3.13. Essas propriedades são semelhantes às correspondentes para “vizinhanças”. Dizer que $X \in τ_{X}$ é o mesmo que dizer que todo ponto tem ao menos uma vizinhança (aberta).

4.2 Deﬁnição

Agora que, na medida do possível, devidamente motivados, vamos deﬁnir o que vem a ser uma topologia em um conjunto $X$ qualquer.

Deﬁnição 4.1 (Espaço Topológico).

Seja $X$ um conjunto qualquer. Dizemos que uma família $τ_{X} \subset 𝒫 (X)$ deﬁne uma topologia no espaço $X$ , ou que $(X, τ_{X})$ é um espaço topológico, quando $τ_{X}$ satisfaz:

$\emptyset, X \in τ_{X}$ .

A família

τ_{X}

é fechada por interseção ﬁnita:

A, B \in τ_{X} \Rightarrow A \cap B \in τ_{X} .

A família $τ_{X}$ é fechada por união arbitrária:
$A_{λ} \in τ_{X} (λ \in Λ) \Rightarrow ⋃_{λ \in Λ} A_{λ} \in τ_{X} .$

Os subconjuntos $A \subset X$ tais que $A \in τ_{X}$ são chamados de abertos do espaço topológico $(X, τ_{X})$ . Por um abuso de notação, quando conveniente, dizemos que $X$ é um espaço topológico.

A topologia de um espaço métrico, deﬁnida em 3.11 é de fato, pela Proposição 3.13, uma topologia no sentido da Deﬁnição 4.1. Vejamos outros exemplos de topologia.

4.2.1 Exemplos

Exemplo 4.2 (Topologia Discreta).

Dado um conjunto qualquer $X$ , $(X, 𝒫 (X))$ é um espaço topológico. Esta topologia é induzida, por exemplo, pela métrica discreta mencionada no Exemplo 1.9.

Exemplo 4.3 (Topologia Trivial (caótica)).

Dado um conjunto qualquer $X$ , $(X, {\emptyset, X})$ é um espaço topológico. Se o conjunto $X$ tiver mais do que um elemento, essa topologia nunca é dada (induzida) por uma métrica, pois não satisfaz a Proposição 1.6.

Exemplo 4.4 (Topologia da Continuidade Inferior).

Considere os números reais $ℝ$ e a seguinte família de subconjuntos de $ℝ$

τ_{} = \{(α, \infty)| α \in ℝ\} .

Neste caso, $(ℝ, τ_{})$ é um espaço topológico. Assim como no Exemplo 4.3, essa topologia também não é induzida por uma métrica.

Do mesmo modo, existe a topologia da Continuidade Superior, dada por

τ_{} = \{(- \infty, α)| α \in ℝ\} .

Exemplo 4.5 (Topologia Inicial).

Seja $X$ um conjunto e $(Y, τ_{Y})$ um espaço topológico. Considere uma aplicação $f : X \to Y$ qualquer. Então $(X, f^{- 1} (τ_{Y}))$ é um espaço topológico.

4.3 Vizinhanças e Base de Vizinhanças de um Ponto

Assim como ﬁzemos para espaços métricos, podemos deﬁnir para um espaço topológico $(X, τ_{X})$ , o que é para cada ponto $x \in X$ , a família de todas as suas vizinhanças.

Deﬁnição 4.6.

Seja $(X, τ_{X})$ um espaço topológico. Dado $x \in X$ , uma vizinhança aberta de $x$ é um aberto $A \in τ_{X}$ que contém o ponto $x$ . Uma vizinhança de $x$ é qualquer conjunto que contenha uma vizinhança aberta de $x$ . Denotamos por $𝒱_{} (x)$ a família de todas as vizinhanças de $x$ .

Observação 4.7. Alguns autores usam o termo vizinhança para designar apenas as vizinhanças abertas. Provavelmente, a causa disso, é a sobrevalorização dos conjuntos abertos. Em muitos casos, onde seria melhor considerar vizinhanças, muitos matemáticos insistem em enxergar apenas os conjuntos abertos. Neste livro, se quisermos uma vizinhança aberta de $x$ , diremos “vizinhança aberta de $x$ ”, ou simplesmente, “um aberto que contém $x$ ”. Caso contrário, diremos apenas vizinhança para o que outros autores chamariam de “um conjunto que contém uma vizinhança aberta de $x$ ”.

Em um espaço topológico qualquer, as vizinhanças de um ponto possuem as mesmas propriedades para o caso de espaços métricos que as descritas na Proposição 3.4.

Proposição 4.8.

Seja $X$ um espaço topológico, e $x \in X$ um ponto de $X$ . Então valem as seguintes aﬁrmações sobre a família $𝒱_{} (x)$ de todas as vizinhanças de $x$ :

Se $A \in 𝒱_{} (x)$ e $A \subset B$ , então $B \in 𝒱_{} (x)$ .
A interseção de duas vizinhanças de $x$ também é uma vizinhança de $x$ . Ou seja, se $A, B \in 𝒱_{} (x)$ , então $A \cap B \in 𝒱_{} (x)$ .
Se $A \in 𝒱_{} (x)$ então existe $B \subset A$ tal que $x \in B$ , e $B$ é vizinhança de todos os seus pontos.

Demonstração. Todos os itens são evidentes da deﬁnição de vizinhança. O item (2) é consequência do fato de $τ_{X}$ ser fechado por interseção ﬁnita. □

Assim como no caso de espaços métricos, podemos caracterizar os conjuntos abertos como sendo aqueles que são vizinhanças de todos os seus pontos.

Proposição 4.9.

Dado um espaço topológico $X$ , um conjunto $A \subset X$ é aberto se, e somente se, for vizinhança de todos os seus pontos.

Demonstração. Pela deﬁnição de vizinhança, um conjunto aberto é evidentemente vizinhança de todos os seus pontos. Suponha então que $A \subset X$ é vizinhança de todos os seus pontos. Vamos mostrar que $A$ é aberto.

Por hipótese, para cada $a \in A$ existe um aberto $U_{a}$ tal que $a \in U_{a} \subset A$ . Neste caso,

A = ⋃_{a \in A} U_{a} .

Como $A$ é uma união de abertos $U_{a}$ , temos que $A$ também é aberto. □

Deﬁnição 4.10.

Seja $(X, τ_{X})$ um espaço topológico e $x \in X$ um ponto qualquer de $x$ . Uma família formada por vizinhanças de $x$ , $ℬ \subset 𝒱_{} (x)$ , é chamada de base de vizinhanças de $x$ quando para toda vizinhança $V \in 𝒱_{} (x)$ existir $B \in ℬ$ tal que $B \subset V$ . Se todos os conjuntos de $ℬ$ forem abertos, ou seja, se $ℬ \subset τ_{X}$ , então diremos que $ℬ$ é uma base de vizinhanças abertas de $x$ .

Observação 4.11. Alguns autores dizem base local ao invés de base de vizinhanças.

Agora que, mesmo sem uma métrica, deﬁnimos o que vem a ser uma vizinhança de um ponto, podemos deﬁnir convergência de sequências. As sequências não serão tão importantes para a teoria geral. No entanto, motivarão a deﬁnição de redes; um conceito que será trabalhado no Capítulo ??.

Deﬁnição 4.12.

Seja $(X, τ_{X})$ um espaço topológico e $x_{n} \in X$ uma sequência de elementos de $X$ . Dizemos que $x_{n}$ converge para $x \in X$ na topologia $τ_{X}$ , quando para toda vizinhança $V \in 𝒱_{} (x)$ existir $N = N (V) \in ℕ$ tal que

n \geq N \Rightarrow x_{n} \in V .

De maneira semelhante ao caso dos espaços métricos, denotamos tal fato por $x_{n} \to_{}^{τ_{X}} x$ , ou simplesmente $x_{n} \to x$ .

Observação 4.13. Novamente, como no caso métrico, para saber se uma sequência $x_{n} \in X$ converge para $x \in X$ , basta veriﬁcar a condição da Deﬁnição 4.12 para uma base de vizinhanças de $x$ . Em particular, assim como no caso dos espaços métricos, dados $x_{n}, x \in X$ , teremos que $x_{n} \to_{}^{τ_{X}} x$ se, e somente se,

para toda vizinhança aberta $A$ de $x$ existe $N = N (A) \in ℕ$ tal que

n \geq N \Rightarrow x_{n} \in A .

Isso porque a família das vizinhanças abertas de $x$ formam uma base para $𝒱_{} (x)$ .

4.4 Continuidade em um Ponto

A essas alturas, o leitor já sabe o que será tratado nesta seção. Assim como ﬁzemos para os espaços métricos na Seção 3.2, vamos falar sobre a continuidade de aplicações entre espaços topológicos. O leitor deve comparar a Deﬁnição 4.14 e a Proposição 3.6, que caracteriza continuidade em um ponto em espaços métricos.

Deﬁnição 4.14.

Sejam $X$ e $Y$ espaços topológicos e $f : X \to Y$ uma aplicação qualquer entre $X$ e $Y$ . Para $x \in X$ , dizemos que $f$ é contínua em $x$ quando

f^{- 1} (𝒱_{} (f (x))) \subset 𝒱_{} (x) .

Ou seja, quando a imagem inversa de toda vizinhança de $f (x)$ for uma vizinhança de $x$ .

Em uma formulação mais semelhante aos argumentos do estilo $𝜀 - δ$ , a deﬁnição de continuidade ﬁca assim:

Para todo $V \in 𝒱_{} (f (x))$ existe $U \in 𝒱_{} (x)$ tal que

y \in U \Rightarrow f (y) \in V .

Como no caso de espaços métricos, basta veriﬁcar a condição da deﬁnição para uma base de vizinhanças de $x$ .

Proposição 4.15.

Sejam $X$ e $Y$ espaços topológicos e $f : X \to Y$ uma aplicação qualquer. Dados $x \in X$ e $ℬ$ uma base de vizinhanças de $f (x)$ . Então, $f$ é contínua em $x$ se, e somente se,

f^{- 1} (ℬ) \subset 𝒱_{} (x) .

Demonstração. Se $V \in 𝒱_{} (f (x))$ , então existe $B \in ℬ$ tal que $B \subset V$ . Portanto, $f^{- 1} (V) \supset f^{- 1} (B) \in 𝒱_{} (x)$ . Assim, $f^{- 1} (V) \in 𝒱_{} (x)$ . Como $V$ é um elemento arbitrário de $𝒱_{} (f (x))$ , temos que

f^{- 1} (𝒱_{} (f (x))) \subset 𝒱_{} (x) .

□

4.5 Continuidade

Continuidade é um conceito central em topologia. Uma aplicação contínua transporta aspectos topológicos entre os espaços em questão. Dada uma aplicação $f : X \to Y$ entre os conjuntos $X$ e $Y$ , podemos ver $f^{- 1}$ como uma aplicação

f^{- 1} : 𝒫 (Y) \to 𝒫 (X) .

Se $(X, τ_{X})$ e $(Y, τ_{Y})$ são espaços topológicos e $f$ é contínua em $x \in X$ , podemos olhar para $f^{- 1}$ restrita a $𝒱_{} (f (x))$ como sendo uma aplicação

f^{- 1} : 𝒱_{} (f (x)) \to 𝒱_{} (x) .

A proposição a seguir demonstra que quando $f$ é contínua em todo ponto de $X$ , então a restrição de $f^{- 1}$ a $τ_{Y}$ pode ser vista como uma aplicação

f^{- 1} : τ_{Y} \to τ_{X} .

Proposição 4.16.

Sejam $(X, τ_{X})$ e $(Y, τ_{Y})$ espaços topológicos e $f : X \to Y$ uma aplicação de $X$ em $Y$ . Neste caso, são equivalentes:

A função $f$ é contínua em todo ponto $x \in X$ .
Para todo aberto $A \in τ_{Y}$ , $f^{- 1} (A) \in τ_{X}$ .

Demonstração. Para todo ponto $x \in f^{- 1} (A)$ , $f (x) \in A$ . Então, dado $A \in τ_{Y}$ , temos que para todo ponto $x \in f^{- 1} (A)$ , como $A$ é aberto, $A \in 𝒱_{} (f (x))$ . Pela continuidade de $f$ no ponto $x$ , temos que $f^{- 1} (A) \in 𝒱_{} (x)$ . Acabamos de mostrar que $f^{- 1} (A)$ é vizinhança de todos os seus pontos, e portanto, pela Proposição 4.9, $f^{- 1} (A)$ é um aberto de $X$ .

Por outro lado, para $x \in X$ qualquer, denotando por $ℬ_{f (x)}$ a família dos abertos que contém $f (x)$ , como a imagem inversa desses abertos contém $x$ , temos que

f^{- 1} (ℬ_{f (x)}) \subset 𝒱_{} (x) .

E como $ℬ_{f (x)}$ é uma base de $𝒱_{} (f (x))$ , temos que

f^{- 1} (𝒱_{} (f (x))) \subset 𝒱_{} (x) .

Ou seja, $f$ é contínua em $x$ . □

Deﬁnição 4.17 (Função Contínua). Dizemos que uma função $f : X \to Y$ entre os espaços topológicos $(X, τ_{X})$ e $(Y, τ_{Y})$ é contínua quando é contínua em todo ponto $x \in X$ . Ou, equivalentemente, quando $f^{- 1} (τ_{Y}) \subset τ_{X}$ .

4.5.1 Homeomorﬁsmos

Para dois conjuntos $X$ e $Y$ , uma bijeção $f : X \to Y$ identiﬁca cada ponto de $X$ a um único ponto de $Y$ e vice-versa. Se $X$ e $Y$ forem espaços topológicos, $f$ for contínua e sua inversa $f^{- 1} : Y \to X$ também for contínua, então também serão identiﬁcados cada aberto de $X$ com um único aberto de $Y$ e vice-versa. Tudo o que puder ser dito sobre a topologia de $X$ poderá ser aﬁrmado sobre a topologia de $Y$ através da identiﬁcação dada por $f$ .

Deﬁnição 4.18 (Homeomorﬁsmo).

Sejam $X$ e $Y$ espaços topológicos. Dizemos que uma aplicação

f : X \to Y

é um homeomorﬁsmo de $X$ em $Y$ quando $f$ for bijetiva, contínua e sua inversa $f^{- 1}$ também for contínua.

Quando existe um homeomorﬁsmo entre dois espaços topológicos, dizemos que estes espaços são homeomorfos.

4.5.2 Aplicação Aberta

Com uma aplicação $f : X \to Y$ entre espaços topológicos, podemos tentar relacionar as topologias de $(X, τ_{X})$ e $(Y, τ_{Y})$ . Se $f$ for um homeomorﬁsmo, sabemos que $X$ e $Y$ possuem exatamente a mesma topologia quando os pontos de $X$ são identiﬁcados com os de $Y$ através de $f$ . Se $f$ for uma bijeção contínua, podemos identiﬁcar cada elemento de $X$ com um único elemento de $Y$ . Com esta identiﬁcação, teremos que $τ_{Y} \subset τ_{X}$ . Uma outra propriedade que $f$ pode ter, que ajudaria a relacionar os espaços $X$ e $Y$ é a de levar abertos de $X$ em abertos de $Y$ . Neste caso, dizemos que $f$ é uma aplicação aberta.

Deﬁnição 4.19.

Seja $f : (X, τ_{X}) \to (Y, τ_{Y})$ uma aplicação entre os espaços topológicos $X$ e $Y$ . Dizemos que $f$ é uma aplicação aberta quando $f (τ_{X}) \subset τ_{Y}$ .

Um homeomorﬁsmo é uma bijeção contínua e aberta. Nossa motivação para a deﬁnição de aplicação aberta é simplesmente imaginar, ignorando o fato de que $f$ pode nem mesmo ser bijetiva, o que seria necessário para que $f^{- 1}$ seja contínua. Mais adiante, veremos maneiras de se transportar topologias de um espaço topológico a um conjunto qualquer através de aplicações entre eles. Quando temos uma bijeção entre um espaço topológico e um conjunto qualquer, ﬁca fácil transportar a topologia de um para o outro. Imagine que $f : X \to Y$ , não uma bijeção, mas uma sobrejeção do espaço topológico $X$ no espaço topológico $Y$ . Podemos deﬁnir o conjunto

\tilde{X} = \{f^{- 1} (y)| y \in Y\},

que nada mais é do que “agrupar” todos os elementos de $X$ que têm a mesma imagem. A projeção natural de $X$ em $\tilde{X}$ é dada por

\begin{matrix} π : & X & \to & \tilde{X} \\ x & \mapsto & f^{- 1} (f (x)) \end{matrix} .

A projeção leva um elemento $x \in X$ na “classe” formada por todos os elementos de $X$ que tem, por $f$ , a mesma imagem que $x$ . A aplicação $f$ pode ser fatorada, de modo que o seguinte diagrama é comutativo (ou seja, $f = \tilde{f} \circ π$ ):

Basta deﬁnir $\tilde{f} (f^{- 1} (y)) = y$ . Agora, $\tilde{f}$ é uma bijeção. Faz sentido esperar que a topologia de $X$ possa ser transportada para $\tilde{X}$ , de modo que as propriedades topológicas de $f$ possam ser investigadas em função de $\tilde{f}$ e vice-versa. Em particular, se $f$ for contínua e aberta, podemos esperar que $\tilde{f}$ seja um homeomorﬁsmo entre $Y$ e $\tilde{X}$ (Veja o exercício ??). Trataremos desse tipo de topologia, a topologia quociente, no Capítulo 7.

Assim como podemos falar de continuidade em um ponto, podemos também deﬁnir o que seria dizer que $f : X \to Y$ é aberta em $x \in X$ . Assim como no caso de continuidade, a deﬁnição ﬁca melhor se usarmos vizinhanças de $x$ ao invés de abertos.

Deﬁnição 4.20.

Seja $f : (X, τ_{X}) \to (Y, τ_{Y})$ uma aplicação entre os espaços topológicos $X$ e $Y$ . Dizemos que $f$ é uma aplicação aberta em $x \in X$ quando $f (𝒱_{} (x)) \subset 𝒱_{} (f (x))$ .

Capítulo 4Motivação e Deﬁnições