8 Conexidade

Deﬁnição 8.1 (Conexidade).

Um espaço topológico $X$ é conexo quando não puder ser escrito como união disjunta não trivial de abertos. Ou seja, se

X = ⋃_{λ \in Λ} A_{λ},

onde todos os $A_{λ}$ são abertos, não-vazios e disjuntos, então $# Λ \leq 1$ .

Um subconjunto de um espaço topológico é conexo quando for conexo na topologia induzida. Um subconjunto que não é conexo é desconexo.

Exemplo 8.2.

Um intervalo $I \subset ℝ$ é um conjunto que satisfaz

a, b \in I, a < x < b \Rightarrow x \in I .

Se $Y \subset ℝ$ não é um intervalo, então não é conexo. De fato, tome $a, b \in Y$ e $x \notin Y$ com $a < x < b$ . Então $Y = (Y \cap (- \infty, x)) \cup (Y \cap (x, \infty))$ , e portanto, $Y$ é desconexo.

Em um espaço conexo

X

, um argumento padrão consiste em mostrar que os pontos

x \in X

que satisfazem determinada propriedade

P (x)

formam um aberto, e os pontos que não satisfazem

P (x)

também formam um aberto. Como o espaço não é união disjunta não-trivial de abertos, ou teremos que todos os pontos satisfazem

P (x)

, ou que nenhum ponto satisfaz

P (x)

Exemplo 8.3.

Seja $A \subset ℝ^{n}$ um aberto conexo. Então, dois pontos quaisquer de $A$ podem ser ligados por um “caminho contínuo” em $A$ . Ou seja, dados $a, b \in A$ , existe $f : [0, 1] \to A$ contínua, com $f (0) = a$ e $f (1) = b$ . Vamos apenas esboçar a demonstração. Os pormenores da demonstração ﬁcam como exercício.

Seja $C$ o conjunto dos pontos que podem ser ligados a $a$ . Então, $C$ é aberto. De fato, se $c \in C$ , tomando $𝜀 > 0$ tal que $B_{𝜀} (c) \subset A$ , temos que todos os pontos $b \in B_{𝜀} (c)$ podem ser ligados a $c$ por um “caminho retilíneo”. Assim, “concatenando” o caminho de $a$ até $c$ com o caminho de $c$ até $b$ , temos um caminho de $a$ até $b$ . Portanto, $B_{𝜀} (c) \subset C$ . Ou seja, $C$ é aberto.

Por outro lado, se $c \notin C$ , tomando novamente $𝜀 > 0$ tal que $B_{𝜀} (c) \subset A$ , temos que nenhum ponto de $B_{𝜀} (c)$ pode ser ligado a $a$ (por quê?). Ou seja, $A \cap C c$ é aberto. Como $a \in C$ , $C$ é não-vazio. Assim, podemos concluir pela conexidade de $A$ que $C = A$ .

Exemplo 8.4.

Mais adiante (Proposição 8.9), mostraremos que os intervalos são conexos na topologia usual de $ℝ$ .

Para $t \in [0, 1]$ , considere uma família de curvas

α_{t} : 𝕊 1 \to ℂ * .

Seja $N : [0, 1] \to ℤ$ o “número total de voltas” que a curva $α_{t}$ faz em torno da origem. Imagine que de alguma forma saibamos que $N (t)$ é contínua. Então, o “número total de voltas” é o mesmo para todas as curvas $α_{t}$ . De fato, o intervalo $[0, 1]$ pode ser escrito como

[0, 1] = ⋃_{n \in ℤ} N^{- 1} (n) .

Como $ℤ$ é discreto, todo subconjunto de $ℤ$ é aberto. Assim, pela continuidade de $N (t)$ , os conjuntos $N^{- 1} (n)$ são todos abertos (e disjuntos). Pela conexidade do intervalo $[0, 1]$ , existe $n_{0} \in ℤ$ tal que

[0, 1] = N^{- 1} (n_{0}) .

Exemplo 8.5. Nenhum subconjunto de $ℚ$ com mais de um elemento é conexo (na topologia induzida da topologia usual de $ℝ$ ). De fato, seja $S \subset ℚ$ , com $a, b \in S$ distintos. Escolha $c \in ℝ ∖ ℚ$ entre $a$ e $b$ . Então,

S = (S \cap (- \infty, c)) \cup (S \cap (c, \infty)) .

Note que esse exemplo é um caso particular do Exemplo 8.2. O que de fato ﬁzemos, foi mostrar que $S$ não é um intervalo, escolhendo $c \notin S$ entre $a$ e $b$ . Por ter essa propriedade, de que todos os conjuntos com mais de um elemento são desconexos, dizemos que $ℚ$ é totalmente desconexo.

Como de costume, vamos ver maneiras diferentes para dizer se um conjunto é ou não conexo. Note que em um espaço topológico

X

, os conjuntos

\emptyset

X

são abertos e fechados ao mesmo tempo. Diremos que um conjunto

F \subset X

é aberto e fechado não-trivial quando for diferente de

\emptyset

X

Proposição 8.6.

Seja $(X, τ_{X})$ um espaço topológico. Então, são equivalentes:

$X$ é conexo.
Não existem $U, V \in τ_{X}$ não-vazios e disjuntos tais que $X = U \cup V$ .
Não existe $A ⊊ X$ aberto e fechado não trivial. Ou seja, os únicos subconjuntos de $X$ que são abertos e fechados ao mesmo tempo são $\emptyset$ e o próprio $X$ .

Se $Y \subset X$ , então são equivalentes:

$Y$ é conexo.
Se $U, V \in τ_{X}$ são tais que $Y \cap U \cap V = \emptyset$ e $Y \subset U \cup V$ , então ou $Y \subset U$ , ou $Y \subset V$ .
Não existem um aberto $A$ e um fechado $F$ tais que
$\emptyset ⊊ A \cap Y = F \cap Y ⊊ Y .$

Demonstração. _ $(1) \Leftrightarrow (2) .$

É evidente que se $X$ for conexo, não podem existir $U$ e $V$ como os do item (2). Por outro lado, se $X$ não for conexo, existe uma família de abertos $A_{λ}$ $(λ \in Λ)$ , com $# Λ > 1$ , não-vazios disjuntos, tais que

X = ⋃_{λ \in Λ} A_{λ} .

Agora é só separar $Λ$ em duas partes não triviais $Λ_{1}$ e $Λ_{2}$ , e fazer

U = ⋃_{λ \in Λ_{1}} A_{λ} e V = ⋃_{λ \in Λ_{2}} A_{λ} .

_ $(2) \Leftrightarrow (3) .$

Basta fazer $A = U$ para obter um conjunto aberto e fechado a partir do item (2). Ou então, fazer $U = A$ e $V = A c$ para obter os conjuntos do item (2) a partir de um aberto e fechado $A$ .

_ $(1) \Leftrightarrow (2) \Leftrightarrow (3) .$

É só usar o fato de que um aberto (um fechado) de $Y$ na topologia induzida é da forma $A \cap Y$ , onde $A$ é um aberto (um fechado) de $X$ . □

Corolário 8.7. Um espaço topológico $X$ é desconexo se, e somente se, todo $x \in X$ for tal que exista um conjunto $F ⊊ X$ aberto e fechado, com $x \in F$ .

Exemplo 8.8. Seja $S \subset ℚ$ , com $a, b \in S$ distintos. Vamos mostrar novamente (veja o Exemplo 8.5) que $S$ não é conexo. Tome $c \in ℝ ∖ ℚ$ entre $a$ e $b$ . Então,

A = (c, \infty) e F = [c, \infty)

satisfazem

\emptyset ⊊ A \cap S = F \cap S ⊊ S .

Contrariando o item (3) da Proposição 8.6.

Como já é esperado, vamos mostrar que os subconjuntos conexos de

ℝ

são exatamente os intervalos.

Proposição 8.9. Um subconjunto de $ℝ$ é conexo se, se somente se, for um intervalo.

Demonstração. No Exemplo 8.2, já mostramos que os conjuntos conexos são intervalos. Vamos mostrar então que todos os intervalos são conexos.

Suponha então que $D \subset ℝ$ é um intervalo desconexo. Sejam $U$ e $V$ abertos como os do item (2) da Proposição 8.6. Escolha $a \in U \cap D$ , e $b \in V \cap D$ . Podemos supor que $a < b$ . Seja $I_{a}$ o maior intervalo aberto tal que

a \in I_{a} \subset U .

Para ver que tal $I_{a}$ existe, basta tomar a união de todos os intervalos abertos que contém $a$ e estão contidos em $U$ . Então, $I_{a} = (s, t)$ , com $t \leq b$ . Como $D$ é um intervalo, $t \in D$ . Além disso, pela maximalidade de $I_{a}$ , temos que $t \notin U$ . Assim,

[a, t) \subset U \cap D e t \in V \cap D .

Mas como $V$ é vizinhança de $t$ , e $t$ está no fecho de $[a, t)$ , temos que $V \cap [a, t) \neq \emptyset$ . Em particular, $V \cap U \cap D \neq \emptyset$ . Contrariando a escolha de $U$ e $V$ . □

8.2 Conexidade e Continuidade

A propriedade mais importante dos conjuntos conexos é que sua imagem por aplicações contínuas é também conexa. Já utilizamos este fato (de forma oculta) no Exemplo 8.4.

Teorema 8.10.

Seja $f : X \to Y$ uma aplicação contínua. Se $A \subset X$ é conexo, então $f (A)$ é um subconjunto conexo de $Y$ .

Demonstração. Restringindo o domínio e o contra-domínio de $f$ , podemos assumir que $A = X$ , e que $f (A) = Y$ . Se $Y$ não é conexo, então existe $F ⊊ Y$ não-trivial que é aberto e fechado. Pela continuidade de $f$ , $f^{- 1} (F)$ é um subconjunto de $X$ não-vazio que é aberto e fechado. Como $f$ é sobrejetiva, temos que

\emptyset ⊊ f^{- 1} (F) ⊊ X .

Portanto, $X$ não é conexo. □

Uma aplicação contínua

f : (X, τ_{X}) \to (Y, τ_{Y})

é uma aplicação tal que

f^{- 1}

transporta

τ_{Y}

pra dentro de

τ_{X}

. Alternativamente à demonstração anterior, poderíamos ter optado por escolher abertos como os do item (1), (2) ou (3) da Proposição 8.6, e mostrar que esses abertos são levados em abertos de

X

que satisfazem as mesmas condições. Ao reduzir o problema para o caso em que

f

é uma bijeção, o passo seguinte constituiu em mostrar que a imagem inversa de um conjunto desconexo por uma aplicação contínua também é desconexa.

Corolário 8.11 (Teorema do Valor Intermediário).

Seja $I \subset ℝ$ um intervalo qualquer, e $f : I \to ℝ$ uma aplicação contínua. Então, $f (I)$ é um intervalo.

8.3 Propriedades

Por vezes, é importante construir um conjunto e ao mesmo tempo garantir que o conjunto construído será conexo. A maneira mais simples de se fazer isso, é utilizando a proposição que segue.

Proposição 8.12.

Seja $C_{λ}$ uma família de subconjuntos conexos de um espaço topológico $X$ , tal que existe

c \in ⋂ C_{λ} .

Então a união $⋃ C_{λ}$ é um conjunto conexo.

Demonstração. A forma tradicional de se demonstrar é tomando um par de abertos $U$ e $V$ que “particionam” $⋃ C_{λ}$ , e mostrar que esses abertos “particionam” ao menos um dos $C_{λ}$ . Demonstrar dessa forma ﬁca como exercício. Vamos fazer por um outro ângulo. ;-)

Podemos assumir sem perda de generalidade que a união dos $C_{λ}$ é todo o espaço $X$ (porquê?). Suponha, então, que $F \subset X$ é um conjunto que é aberto e fechado com $c \in F$ . Na topologia induzida em $C_{λ}$ , os conjuntos $C_{λ} \cap F$ são abertos e fechados não-vazios, e portanto, são iguais a $C_{λ}$ . Ou seja, $C_{λ} \subset F$ . O que mostra que $F = X$ . □

Proposição 8.13.

Seja $X$ um espaço topológico e $C \subset X$ um subconjunto conexo. Então, qualquer conjunto $D \subset X$ satisfazendo

C \subset D \subset \bar{C}

é conexo.

Demonstração. Novamente, ﬁca como exercício para o leitor utilizar um argumento que envolva um particionamento por abertos como o do item (2) da Proposição 8.6.

Podemos assumir que $D = X$ (por quê?). Seja $F$ um conjunto aberto e fechado não vazio. Por ser aberto, $F$ intersecta $C$ (veja a Seção 6.1). Mas, como $C$ é conexo, temos que $F \cap C = C$ . Ou seja,

C \subset F .

Mas como $F$ é fechado, tomando o fecho, obtemos

X = \bar{C} \subset F .

Portanto, os únicos conjuntos que são abertos e fechados ao mesmo tempo são $\emptyset$ e $X$ . □

Por vezes, nos deparamos com propriedades em classes de conjuntos, que são fechadas por união. Ou seja, se a família de conjuntos

C_{λ}

possui a propriedade, então o conjunto formado pela união dos

C_{λ}

também possui a mesma propriedade. Neste caso, podemos falar do maior conjunto que tem a tal propriedade. No caso de conexidade em espaços topológicos, a Proposição 8.12 nos permite fazer isso. Seja

ℱ_{x}

a família de todos os subconjuntos do espaço topológico que sejam conexos e contenham

x

. Então, pela Proposição 8.12, o conjunto

é conexo e contém

x

. Evidentemente que este é o maior conexo que contém

x

Deﬁnição 8.14 (Componente Conexa). Seja $X$ um espaço topológico, e $x \in X$ um ponto qualquer de $X$ . Então, a componente conexa de $x$ é o maior conexo de $X$ que contém o ponto $x$ .

Proposição 8.15. As componentes conexas particionam um espaço topológico $X$ . Em especial, a relação “ $x$ e $y$ estão na mesma componente conexa” é uma relação de equivalência.

Demonstração. Para um elemento qualquer $x \in X$ , vamos denotar por $C_{x}$ a componente conexa de $x$ . É evidente que $X = ⋃_{x \in X} C_{x}$ . Precisamos mostrar apenas que

y \in C_{x} \Rightarrow C_{x} = C_{y} .

Mas isso é evidente, já que

y \in C_{x} \Rightarrow C_{x} \cup C_{y} é conexo .

□

Proposição 8.16. Em um espaço topológico $X$ , a componente conexa de um ponto $x \in X$ qualquer é fechada.

As componentes conexas de um aberto

A \subset ℝ^{n}

são abertas, mas isso nem sempre acontece em outros espaços topológicos. Os Exemplos 8.5 e 8.8 mostram que as componentes conexas de

ℚ

são conjuntos unitários, que não são abertos na toplogia induzida de

ℝ

ℚ

Exemplo 8.17. Seja $A \subset ℝ$ um aberto, e $C \subset A$ uma componente conexa de $A$ . Vamos veriﬁcar que $C$ é aberto. Para tanto, note que dado $a \in C$ , existe um intervalo (conexo) aberto $V$ , com $a \in V \subset A$ . Pela maximalidade de $C$ , temos que $V \subset C$ . Ou seja, $C$ é vizinhança de todos os seus pontos.

Se, em uma família de espaços topológicos um deles não é conexo, é fácil ver que o produto desses espaços também não é conexo. E se todos forem conexos, será que ainda assim o produto pode ser desconexo?

Proposição 8.18. O produto $X$ de uma família $X_{λ}$ ( $λ \in Λ$ ) de espaços topológicos não vazios é conexo se, e somente se, todos os espaços $X_{λ}$ forem conexos.

Demonstração. Se o produto é conexo, então $X_{λ} = π_{λ} (X)$ é a imagem de um conexo por uma aplicação contínua. Portanto, pelo Teorema 8.10, cada $X_{λ}$ é conexo.

Suponha que todos os $X_{λ}$ são conexos. Tome $x = (x_{λ}) \in X$ . Pela Proposição 7.30, para cada $γ \in Λ$ , os conjuntos

X (γ, x) = ⋂_{\begin{array}{c} λ \in Λ \\ λ \neq γ \end{array}} π_{λ}^{- 1} (x_{λ})

são homeomorfos a $X_{γ}$ , e portanto, são conexos. Note que todos eles contém o elemento $x$ . Pela Proposição 8.12, a união

X (x) = ⋃_{γ \in Λ} X (γ, x)

é conexa. Note que $X (x)$ é o conjunto de todos os elementos de $X$ que diferem de $x$ em no máximo uma entrada.

Seja $u \in X$ um elemento qualquer. Denote por $C_{u}$ a componente conexa de $u$ . Vamos mostrar que $C_{u}$ é denso em $X$ . O argumento anterior, mostra que se $x \in C_{u}$ , então $X (x) \subset C_{u}$ . Por indução, todos os elementos que diferem de $u$ em apenas um número ﬁnito de entradas pertencem a $u$ .

Tome um aberto $A \subset X$ da forma

A = ⋂_{j = 1}^{n} π_{λ_{j}}^{- 1} (A_{j}) .

Esses abertos formam uma base da topologia produto. Seja $a = (a_{λ})$ tal que $a_{λ} \in A_{j}$ para $λ \in \{λ_{1}, \dots, λ_{n}\}$ , e $a_{λ} = u_{λ}$ para $λ \notin \{λ_{1}, \dots, λ_{n}\}$ . Então, $a \in A$ , e $a \in X (u) \subset C_{u}$ . E portanto, $C_{u}$ é denso em $X$ . Como $C_{u}$ é fechado, $C_{u} = X$ . □

8.3.1 Exercícios

8.3.1. Explique o que é a “maximalidade” das componentes conexas mencionadas na demonstração da Proposição 8.16 e no Exemplo 8.17.

8.3.2. Explique melhor a demonstração da Proposição 8.16.

8.3.3. Mostre que se $C$ é um subconjunto conexo de um espaço topológico $X$ , e se $F \subset X$ é um conjunto aberto e fechado que intersecta $C$ , então, $C \subset F$ .

8.3.4. Mostre que um conjunto que é aberto e fechado em um espaço topológico $X$ é união de componentes conexas.

8.3.5. Utilize o Exercício 8.3.4 para concluir que as componentes conexas de um espaço topológico são conjuntos abertos e fechados.

8.3.6. Mostre que as componentes conexas de um aberto $A$ de $[0, 1]$ são intervalos abertos em $[0, 1]$ .

8.3.7. Mostre que as componentes conexas de um aberto $A$ de $ℝ^{n}$ são conjuntos abertos.

8.3.8. Na Proposição 8.12, porque podemos assumir que $X$ é a união de todos os $C_{λ}$ ?

8.3.9. Na Proposição 8.12, por que fazemos a seguinte aﬁrmação?

Na topologia induzida em $C_{λ}$ , $C_{λ} \cap F$ é fechado e aberto.

Não poderíamos simplesmente ter aﬁrmado que $C_{λ} \cap F$ é fechado e aberto?

8.3.10. Na Proposição 8.13, porque podemos assumir que $X = D$ ?

8.4 Conexidade por Caminhos

Os espaços como os do Exemplo 8.3, onde todos os pontos podem ser ligados por um “caminho contínuo”, são os espaços conexos por caminhos. Vamos deﬁnir formalmente e veriﬁcar algumas propriedades interessantes dos espaços conexos por caminhos. Em especial, vamos ver que a conexidade por caminhos é uma propriedade mais forte que a conexidade. Ou seja, todos os espaços conexos por caminhos são conexos.

Deﬁnição 8.19 (Caminho). Seja $X$ um espaço topológico. Um caminho em $X$ é uma aplicação contínua

f : [0, 1] \to X .

Dados $a, b \in X$ , um caminho ligando $a$ a $b$ é um caminho em $X$ tal que $f (0) = a$ e $f (1) = b$ .

Observação 8.20. Uma aplicação contínua $f : I \to X$ , onde $I$ é um intervalo fechado e limitado de $ℝ$ pode ser facilmente transformada em um caminho (com domínio $[0, 1]$ ). Por isso, de agora em diante, vamos usar um certo abuso de linguagem e, neste caso, também vamos dizer que $f$ é um caminho em $X$ .

Proposição 8.21.

Sejam $f$ e $g$ caminhos em um espaço topológico $X$ ligando os pontos $a, b \in X$ e $b, c \in X$ respectivamente. Então, a aplicação

(f * g) (t) = \{\begin{matrix} f (2 t) & , 0 \leq t \leq \frac{1}{2} \\ g (2 t - 1) & , \frac{1}{2} \leq t \leq 1 \end{matrix}

é um caminho em $X$ ligando $a$ e $c$ .

Demonstração. A parte mais difícil é mostrar que $f * g$ é contínua no ponto $\frac{1}{2}$ . Seja $V \subset X$ uma vizinhança de $b = (f * g) (\frac{1}{2})$ Então,

\begin{array}{l} {(f * g)}^{- 1} (V) & = \frac{1}{2} f^{- 1} (V) \cup \frac{1}{2} (1 + g^{- 1} (V)) \\ \supset \frac{1}{2} (α, 1] \cup \frac{1}{2} (1 + [0, β)) \\ = (\frac{α}{2}, \frac{β + 1}{2}) . \end{array}

Portanto, $f * g$ é contínua em $\frac{1}{2}$ . □

A Proposição 8.21 mostra que a relação de “existir um caminho ligando

x

y

é transitiva. Como é evidentemente simétrica e reﬂexiva, é uma relação de equivalência. Cada classe de equivalência dessa relação será uma componente conexa por caminhos.

Deﬁnição 8.22 (Conexidade por Caminhos). Um espaço topológico $X$ é conexo por caminhos quando para quaisquer dois pontos $x, y \in X$ , existir um caminho ligando $x$ a $y$ . Dado $x \in X$ , a componente conexa por caminhos de $x$ é o conjunto de todos os pontos $y \in X$ tais que existe um caminho ligando $x$ a $y$ .

Um subconjunto de um espaço topológico é conexo por caminhos quando o for na topologia induzida.

Proposição 8.23. Em um espaço topológico $X$ , se um conjunto $Y \subset X$ é conexo por caminhos, então é conexo.

Demonstração. Tome $a \in Y$ . Então,

Y = ⋃_{\begin{array}{c} f : caminho em Y \\ f (0) = a \end{array}} f ([0, 1]) .

Os conjuntos $f ([0, 1])$ são conexos por serem imagem do conexo $[0, 1]$ pela aplicação contínua $f$ . Assim, esta é uma união de conjuntos conexos que possuem $a$ como ponto em comum. Pela Proposição 8.12, $Y$ é conexo. □

Sabemos que um conjunto conexo por caminhos é conexo. Vejamos um exemplo de um espaço conexo que não é conexo por caminhos.

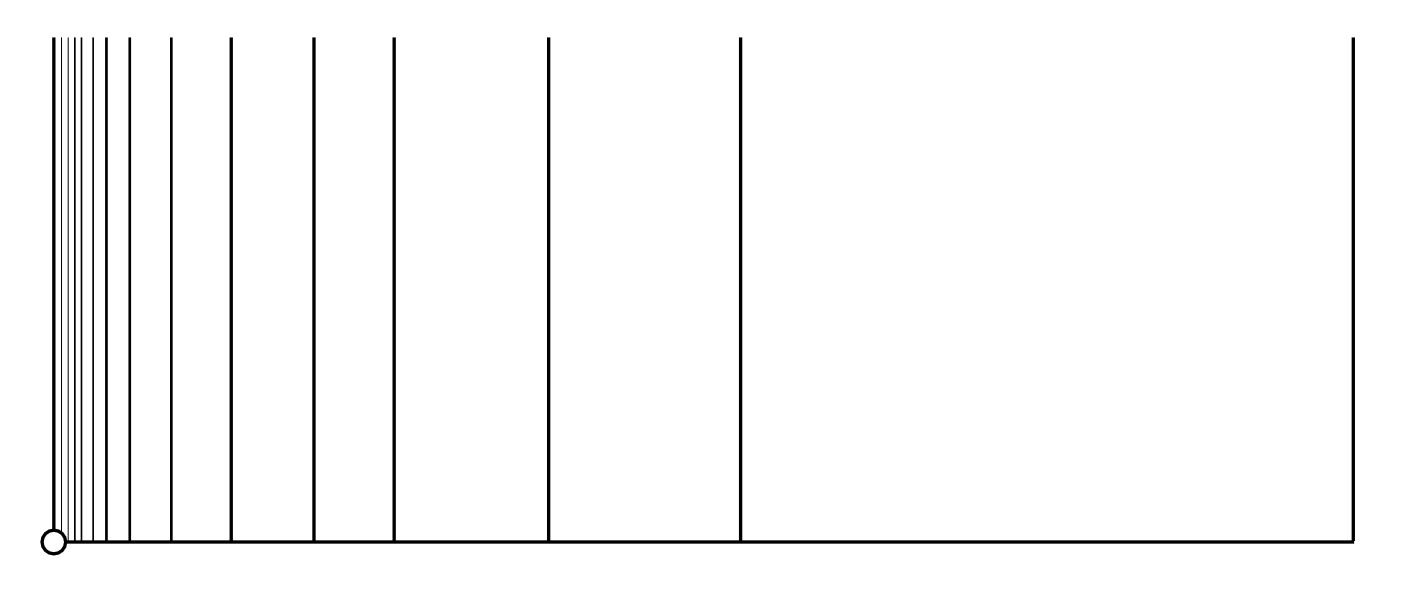
Exemplo 8.24 (Espaço Pente). Seja $K = \{\frac{1}{n}| n = 1, 2, \dots\}$ . Considere os subconjuntos de $ℝ^{2}$

P_{1} = \{0\} \times (0, 1] e P_{2} = ((0, 1] \times \{0\}) \cup (K \times [0, 1]) .

O espaço pente é o conjunto $P = P_{1} \cup P_{2}$ com a topologia induzida de $ℝ^{2}$ . Veja a Figura 8.1. É fácil ver que $P$ é conexo. De fato, como $P_{2}$ é conexo e

P_{2} \subset P \subset \bar{P_{2}},

$P$ é conexo pela Proposição 8.13. No entanto, $P$ não é conexo por caminhos. A demonstração será feita no Exercício 8.4.10 e também no Exemplo ??.

Figura 8.1: Um espaço topológico que é conexo, mas que não é conexo por caminhos.

Uma variação mais simples do espaço pente, é o conjunto

P^{'} = \{(0, 1)\} \cup P_{2} .

Assim como $P$ , $P^{'}$ também é conexo. Suponha que $f : [0, 1] \to P^{'}$ seja um caminho em $P^{'}$ , partindo de $p = (0, 1)$ . Evidentemente que $F = f^{- 1} (p)$ é um fechado de $[0, 1]$ . Vamos mostrar que $F$ também é aberto, para concluirmos que $f$ é um caminho constante. Ou seja, que $p$ não pode ser ligado a nenhum outro ponto de $P_{2}$ por um caminho em $P^{'}$ . Tome $a \in F$ . Seja $B_{p}$ a bola de raio $\frac{1}{2}$ com centro em $p$ . Como $f^{- 1} (B_{p})$ é um aberto que contém $a$ , existe um intervalo fechado $I \subset f^{- 1} (B_{p})$ que é vizinhança de $a$ . Então, $f |_{I}$ é um caminho em $B_{p} \cap P^{'}$ . Mas todos os caminhos em $B_{p} \cap P^{'}$ que passam em $p$ são constantes, pois a componente conexa de $p$ em $B_{p} \cap P^{'}$ é $\{p\}$ . Como $a \in F$ é arbitrário, $F$ é aberto.

8.4.1 Exercícios

8.4.1. Dê um exemplo de um espaço topológico $X$ , com um conexo por caminhos $C \subset X$ , e um conjunto $D \subset X$ que não é conexo por caminhos, mas que seja tal que

C \subset D \subset \bar{C} .

8.4.2. Dê um exemplo de um espaço topológico $X$ que não é conexo por caminhos, mas que contém um conjunto denso $C \subset X$ tal que $C$ é conexo por caminhos.

8.4.3. Mostre que a componente conexa de $B_{p} \cap P^{'}$ do Exemplo 8.24 que contém $p$ é $\{p\}$ .

8.4.4. Mostre que a componente conexa por caminhos que contém um ponto $a$ é o maior conjunto conexo por caminhos que contém $a$ .

8.4.5. Por que na demonstração da Proposição 8.21, a continuidade de $(f * g)$ em pontos distintos de $\frac{1}{2}$ é evidente? Seja, por exemplo, $0 \leq t < \frac{1}{2}$ . Então, se $V$ é uma vizinhança de $(f * g) (t) = f (2 t)$ ,

{(f * g)}^{- 1} (V) \supset \frac{1}{2} f^{- 1} (V)

é vizinhança de $t$ pela continuidade de $f$ de da aplicação $t \mapsto 2 t$ . Pode-se fazer o mesmo para $t > \frac{1}{2}$ .

8.4.6. Por que o argumento da Proposição 8.21 de fato demonstra que $(f * g)$ é contínua em $\frac{1}{2}$ ?

8.4.7. Por quê a componente conexa de $p$ em $B_{p} \cap P^{'}$ é $\{p\}$ ?

8.4.8. Seja $f : [0, 1] \to P$ um caminho no espaço pente do Exemplo 8.24. Mostre que $f^{- 1} (P_{2})$ é aberto.

8.4.9. Seja $f : [0, 1] \to P$ um caminho no espaço pente do Exemplo 8.24. Mostre que $f^{- 1} (P_{1})$ é aberto.

8.4.10. Mostre que o pente $P$ do Exemplo 8.24 não é conexo por caminhos.

8.5 Conexidade Local

As componentes conexas de um espaço topológico são sempre fechadas, mas nem sempre são abertas. Por exemplo,

ℚ

, com a topologia usual (induzida de

ℝ

), é tal que suas componentes conexas são os subconjuntos unitários. No entanto, os conjuntos unitários de

ℚ

não são abertos, haja visto que todo aberto de

ℝ

contém inﬁnitos racionais. Uma propriedade que garante, por exemplo, que as componentes conexas são abertas, é a conexidade local.

Deﬁnição 8.25 (Conexidade Local). Um espaço topológico é localmente conexo quando todo ponto possui uma base de vizinhanças conexas. Se possuir uma base de vizinhanças conexas por caminhos, dizemos que o espaço é localmente conexo por caminhos.

É evidente que um espaço localmente conexo por caminhos é localmente conexo. No Exemplo 8.17, mostramos que as componentes conexas de um aberto de

ℝ

são sempre abertas. A essência da demonstração está no fato de

ℝ

, e consequentemente os abertos de

ℝ

serem espaços localmente conexos. Da mesma forma, o Exemplo 8.3 mostra que as componentes conexas de um aberto de

ℝ

são conexas por caminhos. Novamente, a essência da demonstração se encontra no fato de

ℝ

ser localmente conexo por caminhos.

Proposição 8.26. Seja $A$ um aberto conexo de um espaço topológico localmente conexo por caminhos $X$ . Então, $A$ é conexo por caminhos.

Demonstração. O espaço $A$ , com a topologia induzida, também é localmente conexo por caminhos (por quê?). Portanto, podemos assumir sem perda de generalidade que $A = X$ .

Seja $C$ uma componente conexa por caminhos de $A$ . Como $A$ é localmente conexo por caminhos, $C$ é aberto. Ou seja, $A$ é a união disjunta de suas componentes conexas por caminhos, que são conjuntos abertos. Portanto, pela conexidade de $A$ , só pode existir uma componente conexa por caminhos. □

O espaço pente do Exemplo 8.24 é um exemplo de um espaço conexo que não é localmente conexo. Note que se acrescentarmos o ponto

(0, 0)

ao espaço pente do exemplo, teremos um espaço que é conexo por caminhos mas que não é localmente conexo por caminhos.

8.5.1 Exercícios

8.5.1. Mostre que todas as componentes conexas de um espaço localmente conexo são abertas.

8.5.2. Mostre que em um espaço topológico, as componentes conexas serem abertas equivale a dizer que todo ponto possuí uma vizinhança conexa.

8.5.3. Mostre que em um espaço topológico localmente conexo por caminhos, as componentes conexas por caminhos são abertas e fechadas.

8.5.4. Mostre que em um espaço topológico $X$ localmente conexo por caminhos, as componentes conexas são exatamente iguais às componentes conexas por caminhos.

8.5.5. A demonstração da Proposição 8.26 poderia ter sido feita de um modo um pouco mais “pedestre”. Poderiamos ter tomado $a \in A$ , mostrado que sua componente conexa por caminhos $C$ é aberta, e depois ter tomado $b \in C c$ , e mostrado que existe uma vizinhança $V$ de $b$ , tal que $b \in V \subset C c$ . Para concluirmos que $C c$ é um aberto. Faça esta demonstração mais detalhadamente e compare com a demonstração da Proposição 8.26.

Capítulo 8
Conexidade

8.1 Deﬁnição e Exemplos

8.2 Conexidade e Continuidade

8.3 Propriedades

8.3.1 Exercícios

8.4 Conexidade por Caminhos

8.4.1 Exercícios

8.5 Conexidade Local

8.5.1 Exercícios

Capítulo 8Conexidade

8.1 Deﬁnição e Exemplos

8.2 Conexidade e Continuidade

8.3 Propriedades

8.3.1 Exercícios

8.4 Conexidade por Caminhos

8.4.1 Exercícios

8.5 Conexidade Local

8.5.1 Exercícios

Capítulo 8
Conexidade