1 Deﬁnicao e Propriedades

Capítulo 1
Deﬁnição e Propriedades

Vamos descrever (deﬁnir) o que se entende por espaço métrico (Deﬁnição 1.1), e estudar propriedades desses espaços que nos motivarão a deﬁnir o conceito mais geral de espaço topológico (Deﬁnição 4.1).

Os conhecimentos adquiridos neste capítulo serão importantes para que o leitor possa ter exemplos concretos e também motivação suﬁciente para reconhecer a utilidade e aceitar com naturalidade os conceitos que serão apresentados nos capítulos seguintes.

1.1 Deﬁnição

Um espaço métrico é um conjunto $X$ , munido de uma métrica $d : X \times X \to ℝ +$ . A métrica faz com que esteja deﬁnida uma noção de distância entre os pontos de $X$ .

Deﬁnição 1.1 (Métrica).

Seja $X$ um conjunto qualquer. Uma métrica deﬁnida sobre $X$ é uma função

\begin{matrix} d : & X \times X & \to & ℝ + \\ (x, y) & \mapsto & d (x, y) \end{matrix}

que, para todo $x, y, z \in X$ , satisfaz

$d (x, y) = 0 \Leftrightarrow x = y$ .
$d (x, y) = d (y, x)$ .
$d (x, z) \leq d (x, y) + d (y, z)$ . (desigualdade triangular)

Dizemos que $(X, d)$ é um espaço métrico. Em geral, por um abuso de linguagem, quando a métrica $d$ está subentendida, dizemos que $X$ é um espaço métrico.

Em $ℝ^{n}$ , a métrica usualmente adotada é a métrica euclidiana, dada por

d (x, y) = \sqrt{\sum_{j = 1}^{n} {|x_{j} - y_{j}|}^{2}} .

(1.1)

Onde $x = (x_{1}, \dots, x_{n})$ e $y = (y_{1}, \dots, y_{n})$ .

Em várias situações, o item (1) da deﬁnição de métrica nos permitirá concluir que dois pontos $x, y \in X$ são de fato o mesmo ponto. Basta mostrar que $d (x, y) = 0$ . O item (3) é o mais importante da deﬁnição. É este item que abstrai a idéia de que a distância entre dois pontos está intimamente relacionada com o “menor caminho” entre dois pontos:

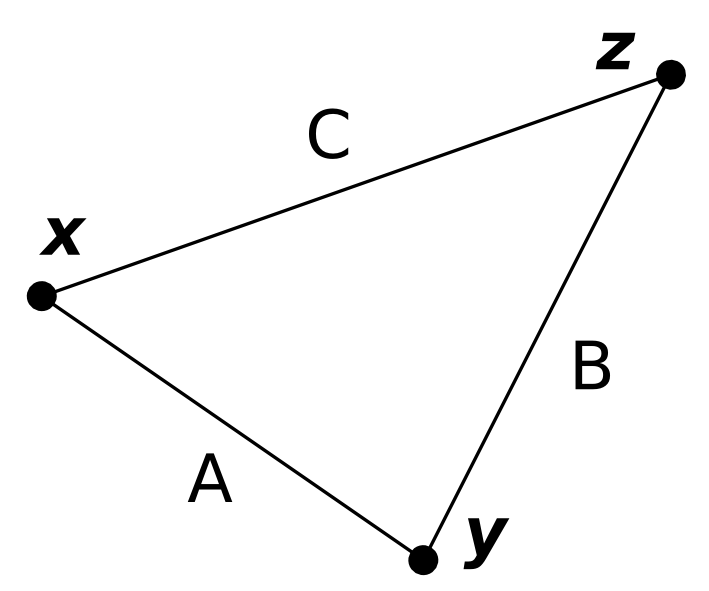
Se existe um caminho $A$ , partindo de $x$ e indo para $y$ , e um caminho $B$ , partindo de $y$ e indo para $z$ , então, a menor distância (ou o ínﬁmo dos comprimentos dos caminhos partindo de $x$ e indo para $z$ ) não é maior do que a soma dos comprimentos de $A$ e $B$ . (Figura 1.1)

Figura 1.1: Desigualdade triangular:

C \leq A + B

Deﬁnição 1.2 (Bola).

Seja $(X, d)$ um espaço métrico, $x \in X$ e $𝜀 > 0$ . A bola de centro $x$ e raio $𝜀$ é o conjunto de todos os pontos que distam de $x$ menos que $𝜀$ :

B_{𝜀} (x) = \{y \in X| d (x, y) < 𝜀\} .

Figura 1.2: A bola de centro

x

e raio

𝜀

1.1.1 Exercícios

1.1.1. Seja $X$ um espaço métrico. Mostre que, $y \in B_{𝜀} (x)$ se, e somente se, $x \in B_{𝜀} (y)$ .

1.1.2. Em um espaço métrico $X$ , mostre que para $x \in X$ e $𝜀 \geq δ > 0$ ,

B_{δ} (x) \subset B_{𝜀} (x) .

1.1.3. Em um espaço métrico $X$ , dado um ponto $x \in X$ e $𝜀 > δ > 0$ distintos, podemos concluir que

B_{δ} (x) ⊊ B_{𝜀} (x) ?

1.1.4. Na deﬁnição de espaço métrico, podemos substituir o item (3)

d (x, z) \leq d (x, y) + d (y, z)

por

d (x, z) \leq d (x, y) + d (z, y) ?

1.1.5.

Na deﬁnição de espaço métrico, podemos substituir o item (2)

d (x, y) = d (y, x)

por

d (x, z) \leq d (y, x) + d (z, y) ?

1.1.6. Mostre que $d : X \times X \to ℝ +$ é uma métrica se, e somente se,

$d (x, y) = 0 \Leftrightarrow x = y$ .
$d (z, x) \leq d (x, y) + d (y, z)$ .

1.1.7. Encontre um exemplo de uma aplicação $d : X \times X \to ℝ +$ satisfazendo

$d (x, y) = 0 \Leftrightarrow x = y$ ; e
$d (x, z) \leq d (x, y) + d (y, z)$ ;

mas que não é uma métrica.

1.1.8. Leia a página da Wikipedia em inglês sobre espaços métricos. Depois, vá até a Wikipedia em português e melhore a página sobre espaços métricos que tem lá. :-)

1.2 Propriedades Elementares

Nesta seção, $(X, d)$ é um espaço métrico. As propriedades mais interessantes dos espaços métricos são conseqüência da desigualdade triangular. Muitas vezes, essas propriedades são mais fáceis de serem visualizadas quando temos em mente a distância euclidiana em $ℝ^{2}$ . Ou seja, quando fazemos um desenho em uma folha de papel. É importante enfatizar no entanto, que os resultados dependem apenas das propriedades das métricas (Deﬁnição 1.1). O desenho melhora a intuição, mas não é uma demonstração.

Todas as proposições deste capítulo são muito simples. O leitor deve ser capaz de completar as demonstrações que aﬁrmam, por exemplo, que basta tomar um certo $δ > 0$ para concluir a demonstração.

Proposição 1.3.

Sejam $x \in X$ e $𝜀 > 0$ . Então existe $n \in ℕ$ tal que

B_{\frac{1}{n}} (x) \subset B_{𝜀} (x) .

Demonstração. Basta tomar $n$ grande o suﬁciente para que $\frac{1}{n} \leq 𝜀$ . □

A seguinte Proposição, apesar de muito simples, é fundamental para o desenvolvimento de toda a teoria que se seguirá, e é conseqüência direta da desigualdade triangular.

Proposição 1.4.

Sejam $x \in X$ , $𝜀 > 0$ e

y \in B_{𝜀} (x) .

Então, existe $δ > 0$ tal que

B_{δ} (y) \subset B_{𝜀} (x) .

Veja a Figura 1.3.

Figura 1.3: Para cada ponto

y

da bola

B_{𝜀} (x)

, temos uma “bolinha” centrada em

y

e toda contida em

B_{𝜀} (x)

Demonstração. Basta tomar $δ < 𝜀 - d (x, y)$ . Neste caso,

\begin{matrix} \begin{aligned} z \in B_{δ} (y) & \Rightarrow d (y, z) < δ \\ \Rightarrow d (x, z) < d (x, y) + δ < 𝜀 \\ \Rightarrow z \in B_{𝜀} (x) . \end{aligned} \end{matrix}

□

Proposição 1.5.

Sejam $x_{1}, x_{2} \in X$ , e $𝜀_{1}, 𝜀_{2} > 0$ . Então, dado $z \in B_{𝜀_{1}} (x_{1}) \cap B_{𝜀_{2}} (x_{2})$ , existe $δ > 0$ tal que

B_{δ} (z) \subset B_{𝜀_{1}} (x_{1}) \cap B_{𝜀_{2}} (x_{2}) .

Veja a Figura 1.4.

Figura 1.4: Para cada ponto

z

da interseção

B_{𝜀_{1}} (x) \cap B_{𝜀_{2}} (y)

, temos uma “bolinha” centrada em

z

e toda contida na interseção.

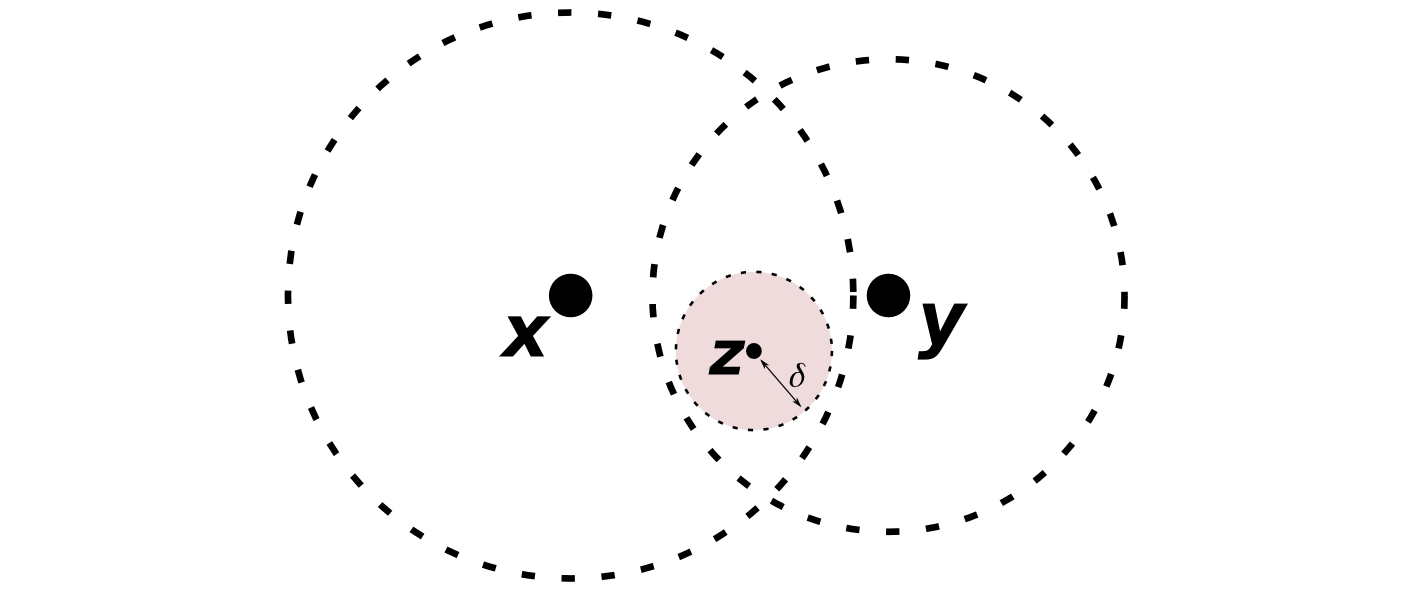
Demonstração. Pela Proposição 1.4, existem $δ_{1}, δ_{2} > 0$ tais que

\begin{array}{rcl} B_{δ_{1}} (z) & \subset & B_{𝜀_{1}} (x_{1}) \\ B_{δ_{2}} (z) & \subset & B_{𝜀_{2}} (x_{2}) . \end{array}

Basta portanto tomar qualquer $δ \leq min (δ_{1}, δ_{2})$ . □

Repare que a proposição “vale” para qualquer número ﬁnito de bolas $B_{𝜀_{1}} (x_{1}), \dots, B_{𝜀_{n}} (x_{n})$ . Mas não “vale” para um número inﬁnito de bolas.

Proposição 1.6.

Sejam $x, y \in X$ dois pontos distintos de $X$ . Então existe $𝜀 > 0$ tal que

B_{𝜀} (x) \cap B_{𝜀} (y) = \emptyset .

Veja a Figura 1.5.

Figura 1.5: Dois pontos distintos

x

y

podem ser “separados” por bolas disjuntas.

Demonstração. Como $x \neq y$ , temos que $d (x, y) > 0$ . Basta tomar

𝜀 \leq \frac{d (x, y)}{2} .

□

Proposição 1.7.

Seja $x \in X$ . Então,

⋂_{𝜀 > 0} B_{𝜀} (x) = {x} .

Demonstração. Basta mostrar que dado $y \in X$ com $y \neq x$ , existe $𝜀 > 0$ tal que

y \notin B_{𝜀} (x) .

Basta tomar $𝜀 \leq d (x, y)$ . Ou então notar que isso segue como um caso particular da Proposição 1.6. □

1.2.1 Exercícios

1.2.1. Mostre que em um espaço métrico $X$ , dado $x \in X$ , temos que

⋃_{0 < δ < 𝜀} B_{δ} (x) = B_{𝜀} (x) .

1.2.2. Seja $X$ um espaço métrico e $x$ um elemento de $X$ . Mostre que para toda sequência ilimitada $n_{k} \in ℕ$ ,

⋂_{k = 1}^{\infty} B_{\frac{1}{n_{k}}} (x) = \{x\} .

1.2.3.

Seja $X$ um espaço métrico, $x_{1}, \dots, x_{n} \in X$ e $𝜀_{1}, \dots, 𝜀_{2}$ números reais maiores que zero. Mostre que se

x \in ⋂_{j = 1}^{n} B_{𝜀_{j}} (x_{j}),

então existe $δ > 0$ tal que

B_{δ} (x) \subset ⋂_{j = 1}^{n} B_{𝜀_{j}} (x_{j}) .

1.2.4. Por que a demonstração do exercício 1.2.3 não vale se o número de bolas não for ﬁnito?

1.2.5. Na demonstração da Proposição 1.7, exatamente quais propriedades da métrica foram utilizadas?

1.2.6. Na demonstração da Proposição 1.6, onde foram utilizadas as seguintes propriedades da métrica?

$d (x, y) = 0 \Rightarrow x = y$ .
$x = y \Rightarrow d (x, y) = 0$ .
$d (x, y) = d (y, x)$ .
$d (x, z) \leq d (x, y) + d (y, z)$ .

1.3 Exemplos

Exemplo 1.8 (Métrica Usual dos Reais (métrica euclidiana)).

Considere o conjunto dos números reais $ℝ$ . A seguinte métrica é a métrica usual dos números reais:

d_{|\cdot|} (x, y) = |y - x| .

O espaço $(ℝ, d_{|\cdot|})$ é um espaço métrico.

Exemplo 1.9 (Métrica Discreta).

Seja $X$ um conjunto qualquer. Então, deﬁnimos a métrica discreta em $X$ por

d_{d} (x, y) = \{\begin{matrix} 0, & x = y \\ 1, & x \neq y \end{matrix} .

Exemplo 1.10 (Métrica Euclidiana de $ℝ^{n}$ ).

Considere o espaço vetorial $ℝ^{n}$ . Agora, deﬁna

d (x, y) = ‖y - x‖,

onde $‖\cdot‖$ é a norma euclidiana de $ℝ^{n}$ . O espaço $(ℝ^{n}, d)$ é um espaço métrico. Além do mais, possui as seguintes propriedades:

Para todo $a, x, y \in ℝ^{n}$ , $d (x + a, y + a) = d (x, y)$ .
Para todo $x, y \in ℝ^{n}$ e $α \in ℝ$ , $d (α x, α y) = |α| d (x, y)$ .

Poderíamos ter feito o mesmo para dois (ou mais) espaços métricos quaisquer, $(A, d_{A})$ e $(B, d_{B})$ , e deﬁnido a seguinte métrica em $A \times B$ :

d ((a_{1}, b_{1}), (a_{2}, b_{2})) = \sqrt{d_{A} {(a_{1}, a_{2})}^{2} + d_{B} {(b_{1}, b_{2})}^{2}} .

Exemplo 1.11 (Métrica do Máximo em $ℝ^{n}$ ).

Novamente, considere o espaço vetorial $ℝ^{n}$ . Sejam $x = (x_{1}, \dots, x_{n})$ e $y = (y_{1}, \dots, y_{n})$ elementos de $ℝ^{n}$ . Então, deﬁna

d (x, y) = max_{1 \leq j \leq n} |y_{j} - x_{j}|,

O espaço $(ℝ^{n}, d)$ é um espaço métrico. Nesta métrica, as bolas são na verdade “quadrados”. :-)

Poderíamos ter feito o mesmo para dois (ou mais) espaços métricos quaisquer, $(A, d_{A})$ e $(B, d_{B})$ , e deﬁnido a seguinte métrica em $A \times B$ :

d ((a_{1}, b_{1}), (a_{2}, b_{2})) = max \{d_{A} (a_{1}, a_{2}), d_{B} (b_{1}, b_{2})\} .

Exemplo 1.12 (Métrica da Soma em $ℝ^{n}$ ).

Novamente, considere o espaço vetorial $ℝ^{n}$ . Sejam $x = (x_{1}, \dots, x_{n})$ e $y = (y_{1}, \dots, y_{n})$ elementos de $ℝ^{n}$ . Então, deﬁna

d (x, y) = \sum_{1 \leq j \leq n} |y_{j} - x_{j}|,

O espaço $(ℝ^{n}, d)$ é um espaço métrico.

Novamente, poderíamos ter feito o mesmo para dois (ou mais) espaços métricos, $(A, d_{A})$ e $(B, d_{B})$ , e deﬁnido a seguinte métrica em $A \times B$ :

d ((a_{1}, b_{1}), (a_{2}, b_{2})) = d_{A} (a_{1}, a_{2}) + d_{B} (b_{1}, b_{2}) .

Exemplo 1.13 (Os Complexos e o $ℝ^{2}$ ).

Podemos identiﬁcar um número complexo $z = α + β i \in ℂ$ com o elemento $(α, β) \in ℝ^{2}$ . Assim, usando a métrica euclidiana de $ℝ^{2}$ , obtemos a métrica

d (α_{1} + β_{1} i, α_{2} + β_{2} i) = \sqrt{{(α_{2} - α_{1})}^{2} + {(β_{2} - β_{1})}^{2}} .

Exemplo 1.14 (Identiﬁcando Dois Conjuntos).

O que ﬁzemos no Exemplo 1.13, poderia ter sido feito para qualquer aplicação injetiva. Se $(X, d_{X})$ é um espaço métrico, e $f : Y \to X$ é uma injeção partindo de um conjunto qualquer $Y$ , então podemos deﬁnir a seguinte métrica no conjunto $Y$ :

d_{Y} (y_{1}, y_{2}) = d_{X} (f (y_{1}), f (y_{2})) .

Exemplo 1.15 (Restrição a um Subconjunto).

Seja $(X, d)$ um espaço métrico e $A \subset X$ . Então, $(A, d |_{A \times A})$ é também um espaço métrico. De fato, esta construção é exatamente o que foi feito no Exemplo 1.14 onde a identiﬁcação entre $A$ e $X$ é a identidade:

\begin{matrix} id : & A & \to & X \\ a & \mapsto & a \end{matrix} .

Exemplo 1.16. Seja $X$ um conjunto qualquer. Denote por $F$ o conjunto de todas as funções $f : X \to ℝ$ . A seguinte função NÃO é uma métrica em $F$ :

d (f, g) = sup_{x \in X} |g (x) - f (x)| .

Isso porque é possível que $d (f, g) = \infty$ . No entanto, se considerarmos o conjunto $F^{'} = \{f \in F| d (f, 0) < \infty\}$ , onde $0$ representa a função constante de valor $0$ , então $(F^{'}, d |_{F^{'}})$ é um espaço métrico. Note que poderíamos ter usado qualquer outra função no lugar de $0$ .

Sempre podemos fazer isso quando uma função $d : X \times X \to ℝ + \cup {\infty}$ satisfaz, com exceção da possibilidade de assumir o valor $\infty$ , as condições para ser uma métrica listadas na Deﬁnição 1.1. Esse artifício é utilizado por exemplo, em análise funcional, quando se estudam os chamados espaços $L^{p}$ . É importante notar que a função $d : X \times X \to ℝ + \cup {\infty}$ está bem deﬁnida. Apenas não é uma métrica se assumir o valor $\infty$ .

1.3.1 Exercícios

1.3.1. Sejam $(A, d_{A})$ e $(B, d_{B})$ espaços métricos. Mostre que

\begin{matrix} d_{} : & (A \times B) \times (A \times B) & \to & ℝ + \\ ((a_{1}, b_{1}), (a_{2}, b_{2})) & \mapsto & max \{d_{A} (a_{1}, a_{2}), d_{B} (b_{1}, b_{2})\} \end{matrix}

é uma métrica.

1.3.2.

Seja $(X_{λ}, d_{X_{λ}})$ ( $λ \in Λ$ ) uma família de espaços métricos tais que a imagem de $d_{X_{λ}}$ esteja condida em $[0, 1]$ . Seja $X = \prod_{λ \in Λ} X_{λ}$ . Mostre que

\begin{matrix} d_{} : & X \times X & \to & ℝ + \\ ((x_{λ}), (y_{λ})) & \mapsto & sup_{λ \in Λ} d_{X_{λ}} (x_{λ}, y_{λ}) \end{matrix}

é uma métrica.

1.3.3.

Seja $(X_{λ}, d_{X_{λ}})$ ( $λ \in Λ$ ) uma família de espaços métricos. Faça $X = \prod_{λ \in Λ} X_{λ}$ , e deﬁna

\begin{matrix} d_{} : & X \times X & \to & ℝ + \cup \{\infty\} \\ ((x_{λ}), (y_{λ})) & \mapsto & sup_{λ \in Λ} d_{X_{λ}} (x_{λ}, y_{λ}) \end{matrix} .

Fixando $a \in X$ , e deﬁnindo

\tilde{X} = \{x \in| d_{} (a, x) < \infty\},

mostre que, $(\tilde{X}, d_{})$ é um espaço métrico.

1.3.4.

Seja $(X_{λ}, d_{X_{λ}})$ ( $λ \in Λ$ ) uma família de espaços métricos. Faça $X = \prod_{λ \in Λ} X_{λ}$ , e deﬁna

\begin{matrix} d_{} : & X \times X & \to & ℝ + \cup \{\infty\} \\ ((x_{λ}), (y_{λ})) & \mapsto & \sum_{λ \in Λ} d_{X_{λ}} (x_{λ}, y_{λ}) \end{matrix} .

Fixando $a \in X$ , e deﬁnindo

\tilde{X} = \{x \in| d_{} (a, x) < \infty\},

mostre que, $(\tilde{X}, d_{})$ é um espaço métrico.

1.3.5. Sejam $(X_{n}, d_{X_{n}})$ , $n \in ℕ$ espaços métricos onde a imagem de $d_{X_{n}}$ esteja condida em $[0, 1]$ . Seja $X = \prod_{n = 1}^{\infty} X_{n}$ . Mostre que

\begin{matrix} d_{} : & X \times X & \to & ℝ + \\ ((x_{n}), (y_{n})) & \mapsto & \sum_{n = 1}^{\infty} \frac{1}{2^{n}} d_{X_{n}} (x_{n}, y_{n}) \end{matrix}

é uma métrica.

1.3.6. De um exemplo de uma aplicação

d_{} : ℝ^{2} \to ℝ +

que satisfaz $x = y \Rightarrow d_{} (x, y) = 0$ , e que também satisfaz os itens (2) e (3) da Deﬁnição 1.1, mas que não é uma métrica.

1.3.7.

Considere a aplicação

\begin{matrix} d_{} : & [0, 1) \times [0, 1) & \to & ℝ + \\ (x, y) & \mapsto & \{\begin{matrix} 1 & , x = 0, y \neq 0 \\ |x - y| & , caso contrário . \end{matrix} \end{matrix}

Mostre que $d_{}$ satisfaz os itens (1) e (3) da Deﬁnição 1.1, mas não é uma métrica.

Capítulo 1Deﬁnição e Propriedades

1.1 Deﬁnição

1.1.1 Exercícios

1.2 Propriedades Elementares

1.2.1 Exercícios

1.3 Exemplos

1.3.1 Exercícios

Capítulo 1
Deﬁnição e Propriedades