2 Topologia Usando uma Metrica

Seja

n \in ℕ

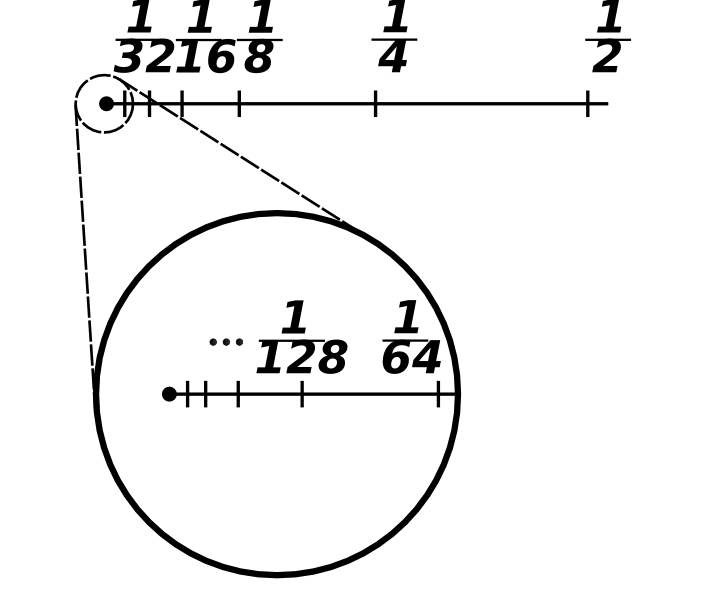
. A sequência de pontos

x_{n} = \frac{1}{n}

é tal que, “na medida que

n

se torna suﬁcientemente grande, a sequência

x_{n}

se aproxima de

0

”. Nesta sessão, vamos formalizar o que entendemos por:

Para um espaço métrico

X

, a noção de “se aproxima de” é um tanto quanto natural, já que temos uma métrica que nos dá uma noção de distância. A grosso modo,

x_{n} \in X

se aproxima de

x

quando a distância entre

x_{n}

x

d (x_{n}, x)

, se aproxima de

0

. Faltaria então deﬁnir o que signiﬁca dizer que a sequência de números reais

d (x_{n}, x)

“se aproxima” de

0

Deﬁnição 2.1 (Convergência).

Sejam $(X, d)$ um espaço métrico e $x_{n} \in X$ ( $n \in ℕ$ ) uma sequência de pontos de $X$ . Dizemos que $x_{n}$ converge para um certo $x \in X$ , quando para todo $𝜀 > 0$ , existir $N \in ℕ$ tal que

n \geq N \Rightarrow d (x_{n}, x) < 𝜀 .

Denotamos tal fato por

x_{n} \to x,

ou por $x_{n} \to_{}^{d} x$ se quisermos enfatizar que a convergência é na métrica $d$ .

Também dizemos que $x$ é o limite da sequencia $x_{n}$ e escrevemos $x = lim x_{n}$ .

A Deﬁnição 2.1 generaliza o que já fazemos para os números reais. No caso dos números reais, usualmente adotamos a métrica

d (x, y) = |y - x|

Deﬁnição 2.2 (Convergência usual em $ℝ$ ).

Seja $α_{n} \in ℝ$ ( $n \in ℕ$ ). Dizemos que $α_{n}$ converge para $α \in ℝ$ , e denotamos tal fato por $α_{n} \to α$ , quando para todo $𝜀 > 0$ , existir $N \in ℕ$ tal que

n \geq N \Rightarrow |α - α_{n}| < 𝜀 .

Poderíamos ter tomado um outro caminho. Já de posse da deﬁnição 2.2, poderíamos ter deﬁnido convergência em espaços métricos de acordo com a seguinte proposição.

Proposição 2.3. Seja $x_{n} \in X$ uma sequencia. Faça $d_{n} = d (x_{n}, x)$ . Então

x_{n} \to x \Leftrightarrow d_{n} \to 0 .

Onde a convergência do lado direito é dada pela Deﬁnição 2.2 ou, equivalentemente, pela métrica euclidiana em $ℝ$ .

Demonstração. É evidente, pois $d (x_{n}, x) \to 0$ se, e somente se, para todo $𝜀 > 0$ , existir $N \in ℕ$ tal que

n \geq N \Rightarrow d (x_{n}, x) < 𝜀 .

□

Proposição 2.4. Seja $x_{n} \in X$ uma sequencia e $x \in X$ . Então são equivalentes:

A sequência converge para $x$ : $x_{n} \to x$ .
Para todo $𝜀 > 0$ , existe $N \in ℕ$ tal que $n \geq N \Rightarrow x_{n} \in B_{𝜀} (x)$ .
Para todo $m \in ℕ$ , existe $N \in ℕ$ tal que $n \geq N \Rightarrow x_{n} \in B_{\frac{1}{m}} (x)$ .

Demonstração. A equivalência entre os itens (2) e (3) segue da Proposição 1.3.

Para a equivalência entre (1) e (2), basta notar que $x_{n} \in B_{𝜀} (x) \Leftrightarrow d (x_{n}, x) < 𝜀$ , e então fazer a substituição na Deﬁnição 2.1. □

Deﬁnição 2.5 (Métricas topologicamente equivalentes). Enquanto não deﬁnimos o que é uma topologia, vamos dizer que duas métricas $d_{1}$ e $d_{2}$ sobre $X$ determinam a mesma topologia (são topologicamente equivalentes) quando

x_{n} \to_{}^{d_{1}} x \Leftrightarrow x_{n} \to_{}^{d_{2}} x .

O objetivo da primeira parte deste livro é o de dar motivação para os conceitos de topologia geral que serão apresentados na segunda parte. A este propósito serve a Proposição 2.4, que apresenta maneira alternativas de se olhar para a convergência de sequencias em espaços métricos. Na medida em que substituímos a métrica

d (x_{n}, x)

pela bola

B_{𝜀} (x)

, as formulações ﬁcam mais parecidas com suas correspondentes para espaços topológicos gerais

2.1.1 Exercícios

2.1.2. Não é imediato da deﬁnição de convergência que o limite de uma sequência, quando existir, será único. Ou seja, a princípio, não há garantias de que $x_{n} \to x$ e $x_{n} \to y$ implique que $x = y$ . Demonstre a unicidade do limite de sequências em espaços métricos.

2.1.4.

Considere a aplicação

\begin{matrix} d_{} : & {[0, 1]}^{ℕ} & \to & ℝ + \\ ((x_{j}), (y_{j})) & \mapsto & \sum_{j = 1}^{\infty} \frac{1}{2^{j}} |x_{j} - y_{j}| \end{matrix} .

Mostre que nesta métrica, para $x^{n} = (x_{j}^{n}) \in {[0, 1]}^{ℕ}$ , $x_{n} \to x = (x_{j}) \in {[0, 1]}^{ℕ}$ se, e somente se, para todo $j \in ℕ$ , $x_{j}^{n} \to x_{j}$ .

2.1.5. Considere a aplicação

\begin{matrix} d_{} : & {[0, 1]}^{ℕ} & \to & ℝ + \cup \{\infty\} \\ ((x_{j}), (y_{j})) & \mapsto & \sum_{j = 1}^{\infty} |x_{j} - y_{j}| \end{matrix} .

E seja

X = \{x \in {[0, 1]}^{ℕ}| d_{} (x, 0) < \infty\} .

Exiba

Uma sequência $x^{n} = (x_{j}^{n}) \in {[0, 1]}^{ℕ}$ tal que $x_{j}^{n} \to x_{j} \in ℝ$ , mas $(x_{j}) \notin X$ .
Uma sequência $x^{n} = (x_{j}^{n}) \in {[0, 1]}^{ℕ}$ tal que $x_{j}^{n} \to x_{j} \in ℝ$ , com $x = (x_{j}) \in X$ , mas que $x^{n} \to̸ x$ .

E reﬂita sobre a inexistência desta patologia no caso do exercício 2.1.4.

2.1.6.

Considere a aplicação

\begin{matrix} d_{} : & {[0, 1]}^{ℕ} & \to & ℝ + \\ ((x_{j}), (y_{j})) & \mapsto & {sup}_{j = 1}^{\infty} |x_{j} - y_{j}| \end{matrix} .

Mostre que nesta métrica, para $x^{n} = (x_{j}^{n}) \in {[0, 1]}^{ℕ}$ , $x^{n} \to x = (x_{j}) \in {[0, 1]}^{ℕ}$ se, e somente se, para todo $𝜀 > 0$ , existe $N \in ℕ$ tal que, independentemente da coordenada $j \in ℕ$ , $n > N \Rightarrow d_{} (x_{j}^{n}, x_{j}) < 𝜀$ .

2.1.7.

Considere a aplicação

\begin{matrix} d_{} : & {[0, 1]}^{ℕ} & \to & ℝ + \\ ((x_{j}), (y_{j})) & \mapsto & {sup}_{j = 1}^{\infty} |x_{j} - y_{j}| \end{matrix} .

Exiba um exemplo de uma sequência $x^{n} = (x_{j}^{n}) \in {[0, 1]}^{ℕ}$ , tal que $x_{j}^{n} \to x_{j}$ , mas $x^{n} \to̸ x = (x_{j})$ .

2.2 Continuidade

Olhando para o gráﬁco de uma função

f : ℝ \to ℝ

na Figura 2.2, você diria que

f

é contínua em

a

De que modo podemos expressar formalmente o signiﬁcado de

f

ser ou não contínua em

a

? Note que no exemplo da Figura 2.2,

Observação 2.8. A continuidade depende apenas da “topologia” dos espaços considerados. Se $f : X \to Y$ é contínua quando considerados os espaços métricos $(X, d_{X})$ e $(Y, d_{Y})$ , então será contínua nos espaços $(X, d_{X}^{'})$ e $(Y, d_{Y}^{'})$ sempre que as métricas $d_{X}$ e $d_{Y}$ forem equivalentes a $d_{X}^{'}$ e $d_{Y}^{'}$ , respectivamente.

2.2.1 Exercícios

2.2.2.

Seja $X = {[0, 1]}^{ℕ}$ , e considere as métricas $d_{1} ((x_{j}), (y_{j})) = sup_{j \in ℕ} |x_{j} - y_{j}|$ e $d_{2} ((x_{j}), (y_{j})) = \sum_{j \in ℕ} \frac{1}{2^{j}} |x_{j} - y_{j}|$ . Mostre que

\begin{matrix} f : & (X, d_{1}) & \to & (X, d_{2}) \\ x & \mapsto & x \end{matrix}

é contínua, mas sua inversa

\begin{matrix} f^{- 1} : & (X, d_{2}) & \to & (X, d_{1}) \\ x & \mapsto & x \end{matrix}

não é.

2.2.4. Mostre que

\begin{matrix} f : & ℚ & \to & ℝ \\ x & \mapsto & \{\begin{matrix} 0 & , x < \sqrt{2} \\ 1 & , x \geq \sqrt{2} \end{matrix} \end{matrix}

é contínua quando $ℚ$ e $ℝ$ são dotados de suas métricas usuais.

2.2.5. Mostre que quando $ℝ$ é dotado de sua métrica usual,

\begin{matrix} f : & ℝ & \to & ℝ \\ x & \mapsto & \{\begin{matrix} 0 & , x \in ℚ \\ 1 & , x \notin ℚ \end{matrix} \end{matrix}

não é contínua em nenhum ponto racional, mas que $f |_{ℚ}$ é contínua.

2.3 Topologia com Bolas

Até o presente momento, temos trabalhado com sequências. Nesta seção vamos formular os mesmos conceitos utilizando bolas. Para que a transição entre sequências e bolas seja suave, vamos começar reavaliando a Proposição 2.4.

A proposição aﬁrma que dizer que

x_{n}

converge para

x

é o mesmo que dizer que toda bola centrada em

x

contém todos os

x_{n}

, exceto talvez para uma quantidade ﬁnita de índices

n

. Note que na Proposição 2.4 falávamos em “para todo

𝜀 > 0

”, mas isso é o mesmo que dizer “para toda bola”!

Resumindo o que já havia sido feito, temos a seguinte caracterização para a convergência de uma sequência.

Proposição 2.9.

Seja $X$ um espaço métrico e $x_{n} \in X$ uma sequência de elementos de $X$ . Então, $x_{n}$ converge para $x \in X$ se, e somente se, para toda bola $B_{𝜀} (x)$ centrada em $x$ , existir $N \in ℕ$ tal que

n \geq N \Rightarrow x_{n} \in B_{𝜀} (x) .

Demonstração. Veja a Proposição 2.4. □

Proposição 2.10.

Sejam $X$ e $Y$ espaços métricos. Então as seguintes aﬁrmações são equivalentes:

A função $f : X \to Y$ é contínua em $a \in X$ .
Para toda bola $B_{f (a)} = B_{𝜀} (f (a))$ centrada em $f (a)$ , existe uma bola $B_{a} = B_{δ} (a)$ centrada em $a$ , tal que
$f (B_{a}) \subset B_{f (a)} .$
Para toda bola $B = B_{𝜀} (f (a))$ centrada em $f (a)$ , $f^{- 1} (B)$ contém alguma bola centrada em $a$ .

Demonstração. _ (2) $\Leftrightarrow$ (3)

A equivalência entre os itens (2) e (3) é evidente, já que dizer que existe uma bola é o mesmo que dizer que existe $δ > 0$ .

_ (2) $\Rightarrow$ (1)

Vamos mostrar que o item (2) implica na continuidade de $f$ no ponto $a$ de acordo com a Deﬁnição 2.6. Seja $x_{n} \to a$ . Vamos mostrar que $f (x_{n}) \to f (a)$ . Tome uma bola qualquer $B$ centrada em $f (a)$ . Por hipótese, existe uma bola $B_{a}$ centrada em $a$ tal que

f (B_{a}) \subset B .

Pela Proposição 2.9, temos que $x_{n} \in B_{a}$ exceto para um número ﬁnito de índices $n$ . Ou seja, $f (x_{n}) \in f (B_{a}) \subset B$ , exceto para um número ﬁnito de índices. O que pela Proposição 2.9 é o mesmo que dizer que $f (x_{n}) \to f (a)$ .

_ (1) $\Rightarrow$ (3)

Suponha então que o item (3) não vale. Neste caso, existe uma bola $B$ centrada em $f (a)$ tal que $f^{- 1} (B)$ não contém nenhuma bola centrada em $a$ . Para cada $n \in ℕ$ , escolha $x_{n} \in B_{\frac{1}{n}} (a)$ tal que $f (x_{n}) \notin B$ . A sequência $x_{n}$ converge para $a$ (por quê?), mas $f (x_{n})$ não converge para $f (a)$ (por que?). □

Observação 2.11. Repare como o item (2) se assemelha à deﬁnição de continuidade que utiliza argumentos do tipo $𝜀 - δ$ :

Para todo $𝜀 > 0$ , existe $δ > 0$ tal que

d (x, a) < δ \Rightarrow d (f (x), f (a)) < 𝜀 .

Observação 2.12.

Para mostrar que a negação do item (3) implica na não continuidade de $f$ , construímos uma sequência $x_{n} \to a$ tal que $f (x_{n}) \to̸ f (x)$ . Para isso, utilizamos as bolas $B_{\frac{1}{n}} (a)$ e a Proposição 1.3.

2.3.1 Exercícios

2.3.1.

Em um espaço métrico $X$ , dado $x \in X$ , dizemos que $V \subset X$ é uma vizinhança de $x$ quando existir uma bola $B_{𝜀} (x)$ tal que $B_{𝜀} (x) \subset V$ . Vamos denotar por $𝒱_{} (x)$ a família de todas as vizinhanças de $x$ . Mostre que uma aplicação $f : (X, d_{X}) \to (Y, d_{Y})$ é contínua em $x \in X$ se, e somente se,

f^{- 1} (𝒱_{} (f (x))) \subset 𝒱_{} (x) .

Onde

f^{- 1} (𝒱_{} (f (x))) = \{f^{- 1} (V)| V \in 𝒱_{} (f (x))\} .

2.3.2.

Usando a mesma nomenclatura que no exercício 2.3.1, vamos chamar um conjunto $A \subset X$ de aberto quando para todo $x \in A$ valer que $A \in 𝒱_{} (x)$ . Ou seja, um aberto é um conjunto que é vizinhança de todos os seus pontos. Mostre que uma aplicação $f : (X, d_{X}) \to (Y, d_{Y})$ é contínua se, e somente se, para todo aberto $U \subset Y$ , $f^{- 1} (U)$ for um aberto de $X$ .

2.3.3.

Usando a nomenclatura do exercício 2.3.1, mostre que uma sequência $x_{n} \to x$ se, e somente se para toda vizinhança $V$ de $x$ , o conjunto

N_{V} = \{n \in ℕ| x_{n} \notin V\}

é ﬁnito.

2.3.4. Usando a nomenclatura do exercício 2.3.2, mostre que uma sequência $x_{n} \to x$ se, e somente se para todo aberto $A$ contendo $x$ , o conjunto

N_{A} = \{n \in ℕ| x_{n} \notin A\}

é ﬁnito.

Capítulo 2
Topologia Usando uma Métrica

2.1 Seqüências e Convergência

2.1.1 Exercícios

2.2 Continuidade

2.2.1 Exercícios

2.3 Topologia com Bolas

2.3.1 Exercícios

Capítulo 2Topologia Usando uma Métrica

2.1 Seqüências e Convergência

2.1.1 Exercícios

2.2 Continuidade

2.2.1 Exercícios

2.3 Topologia com Bolas

2.3.1 Exercícios

Capítulo 2
Topologia Usando uma Métrica